فهرست مطالب:
- مرحله 1: ایجاد ماتریس مجاورت
- مرحله 2: ایجاد روابط
- مرحله 3: آمار بیماری ها را اضافه کنید
- مرحله 4: احتمال اینکه فرد واکسینه و غیر واکسینه آلوده شود را تصادفی کنید
- مرحله 5: ایجاد ماتریس از افرادی که از اطلاعات اولیه واکسینه نشده اند و آلوده شده اند
- مرحله 6: رسم نمودار اولیه
- مرحله 7: پیشرفت عفونت را شبیه سازی کنید
- مرحله 8: از نظریه مونت کارلو استفاده کنید
- مرحله 9: با شبیه سازی به یک تابع فایل ('infecim.m.m') را بسازید
- مرحله 10: درصد افراد واکسینه نشده و واکسینه شده را که آلوده شده اند محاسبه کنید
- مرحله 11: یک متغیر خروجی در عملکرد خود ایجاد کنید "infeSim.m"
- مرحله 12: ایجاد منو برای دریافت شرایط اولیه شبیه سازی از کاربر
- مرحله 13: یک درصد افراد واکسینه نشده را انتخاب کرده و میانگین افراد واکسینه نشده و آلوده را به درصد انتخاب شده محاسبه کنید
- مرحله 14: نمودار: "روند عفونت در مقابل واکسینه نشده" واکسیناسیون بیماری خاص "
- مرحله 15: محصول نهایی: شبیه سازی چگونه به نظر می رسد

تصویری: واکسینه شدن یا نه؟ پروژه مشاهده ایمنی گله از طریق شبیه سازی بیماری: 15 مرحله

2024 نویسنده: John Day | [email protected]. آخرین اصلاح شده: 2024-01-30 08:57

مروری بر پروژه:
پروژه ما مصونیت گله را بررسی می کند و امیدوار است مردم را تشویق به واکسیناسیون کند تا میزان عفونت در جوامع ما کاهش یابد. برنامه ما شبیه سازی می کند که چگونه یک بیماری با درصد های مختلف نرخ واکسینه و بدون واکسیناسیون جمعیت را آلوده می کند. این نشان می دهد که ایمنی گله نشان می دهد که چگونه افزایش تعداد افراد واکسینه شده می تواند تعداد افراد مبتلا را کاهش دهد.
ما این را در Matlab با استفاده از مفاهیم نظریه گراف مدل می کنیم. نظریه نمودار یک روش ریاضی برای نشان دادن روابط بین اجسام است. در نظریه گراف ، نمودارها دارای رأس (یا گره هایی) هستند که توسط لبه ها (یا خطوط) به هم متصل شده اند. برای پروژه ما ، گره ها افراد مربوطه هستند و لبه ها اتصالات آنها هستند. به عنوان مثال ، اگر دو گره با یک لبه به هم متصل شده باشند ، به این معنی است که آنها "دوست" هستند یا نوعی از تماس با یکدیگر دارند. این تماس راهی برای گسترش بیماری است. به همین دلیل است که ما از نظریه گراف برای مدل سازی مفهوم خود استفاده کردیم زیرا می خواستیم ببینیم چگونه بیماری بین افراد متصل به یک جمعیت گسترش می یابد.
پروژه ما همچنین شامل روش مونت کارلو است. روش مونت کارلو الگوریتم هایی هستند که نمونه گیری تصادفی مکرر را برای دریافت نتایج عددی ایجاد می کنند. در پروژه ما ، ما از این روش برای اجرای شبیه سازی خود چندین بار استفاده می کنیم که درصد واکسیناسیون اولیه را تغییر می دهد تا میزان آلودگی افراد را مشاهده کنیم.
تمام کد پروژه در پایین پیوند خورده است!
اعتبار رایانه:
پیوند Matlab به نظریه نمودار:
مرحله 1: ایجاد ماتریس مجاورت


یک اسکریپت جدید ایجاد کنید. ما قصد داریم نام خود را "infeSim.m" بگذاریم.
ما قصد داریم یک متغیر "NUMOFPEOPLE" ایجاد کنیم. می توانید آن را به هر مقدار صحیح اختصاص دهید. این نشان دهنده تعداد افراد در جمعیت شما خواهد بود.
از این پس فرض می کنیم که
NUMOFPEOPLE = 20 ؛
ابتدا با استفاده از توابع نظریه نمودار Matlab برای یک گراف غیر مستقیم شروع کنید.
اگر علاقه مند به یادگیری بیشتر هستید ، پیوندی در اختیار شما قرار می گیرد تا در مورد آن بیشتر بخوانید.
www.mathworks.com/help/matlab/math/directed-and-undirected-graphs.html
یک ماتریس مجاورت ایجاد کرد.
adjMatrix = صفر (NUMOFPEOPLE) ؛
با این کار یک ماتریس مربع 0 ثانیه ایجاد می شود. هر سطر در ماتریس یک نفر است. هر ستون در ماتریس یک شخص یا دوست است که شخص در طول روز ملاقات می کند.
برای کمک به تجسم ظاهر adjMatrix برای 20 نفر ، به شکل 100 (بالا) مراجعه کنید.
** از این به بعد ما فرض می کنیم که NUMOFPEOPLE برابر 20 است. **
می توانید ترسیم این ماتریس مجاورت را امتحان کنید. در اینجا اطلاعات بیشتری در مورد ترسیم این نوع ماتریس ها آورده شده است.
توجه: ماتریس مجاورت چگونه کار می کند.
سابق:
making ساخت ماتریس مجاور
a = [0 ، 1 ، 0 ، 0 ، 0 ؛ 1 ، 0 ، 1 ، 1 ، 1 ؛ 0 ، 1 ، 0 ، 0 ، 0 ؛ 0 ، 1 ، 0 ، 0 ، 0 ؛ 0 ، 1 ، 0 ، 0 ، 0]٪ رسم g = نمودار (a) ؛ ٪ با استفاده از تابع نمودار (نظریه گراف) شکل (1) ؛ h = نمودار (g) ؛
برای مشاهده نحوه افزودن لبه ها در ماتریس مجاورت ، با استفاده از کد موجود در "توجه" ، شکل 1 (بالا) را ببینید.
مرحله 2: ایجاد روابط

اکنون که افراد (راس ها یا گره ها) ایجاد شده اند ، ما باید شبکه ای از روابط (خطوط یا لبه های نمودار) را ایجاد کنیم. این نحوه تعامل و ملاقات افراد را در طول روز شبیه سازی می کند.
این را می توان به روش های زیادی انجام داد. یکی از راه های تکمیل این کار این است که ابتدا یک عدد تصادفی به هر فرد اختصاص دهید تا مشخص شود هر فرد در یک روز با چند نفر ارتباط برقرار می کند.
numOfFriendsMatrix = randi ([minimumFriendsPersonCanHave، mostFriendsPersonCanHave]، 1، NUMOFPEOPLE)؛
این یک ماتریس 1 در 20 از اعداد صحیح تصادفی را نشان می دهد که تعداد تعاملات هر فرد در روز را نشان می دهد. ستون های این ماتریس تعداد مربوط به هر فرد خواهد بود. به عنوان مثال ، اگر ما حداقل FriendsPersonCanHave = 2 و mostFriendsPersonCanHave = 5 را تعیین کنیم ، مقادیر تصادفی بین 2 تا 5 به دست می آوریم.
با () randi مشکل دارید؟ در ترمینال ، تایپ کنید
به رندی کمک کنید
در مرحله بعد ، ما یک ماتریس تصادفی (به نام "allFriendsmatrix") از نحوه ارتباط/تعامل هر فرد در جمعیت با جمعیت ایجاد می کنیم.
tempMatrix = ؛
تعداد = 0 ؛ allFriendsMatrix = ؛ برای k = 1: NUMOFPEOPLE در حالی که طول (tempMatrix) ~ = numOfFriendsMatrix (k) تعداد = شمارش +1 ؛ temp = رندی ([1 ، NUMOFPEOPLE]) ؛ tempMatrix (تعداد) = temp ؛ پایان هر کدام در حالی که طول (tempMatrix) ~ = 9 tempMatrix = [tempMatrix، NaN]؛ پایان allFriendsMatrix = [allFriendsMatrix؛ tempMatrix]؛ tempMatrix = ؛ تعداد = 0 ؛ پایان
توضیح کامل کد:
ابتدا یک ماتریس موقت خالی برای نگهداری دوستان/لیست تعاملات هر شخص ایجاد می کنیم. ما همچنین شمارش اولیه را انجام می دهیم ، که فقط پیگیری می کند که کجا اتصال تصادفی جدید را در tempMatrix بچسبانیم. حلقه های for 20 بار اجرا می شوند تا این مورد برای هر فرد در جمعیت رخ دهد. حلقه while اول اجرا می شود تا زمانی که tempMatrix هر فرد به همان تعداد از تعداد تعاملات تصادفی اختصاص داده شده باشد. در این حلقه ، یک عدد تصادفی مربوط به فرد در جمعیت ایجاد می شود و در tempMatrix قرار می گیرد. از آنجا که طول هر یک از tempMatrixes متفاوت است ، ما نیاز به ایجاد مقادیر NaN داریم تا بتوانیم همه این tempMaticies را در یک ماتریس به هم متصل کنیم ('allFriendsMatrix'). حلقه while دوم این مشکل را با افزودن NaN به هر tempMatrix حل می کند. حلقه while تنظیم شد که 9 بار اجرا شود زیرا عددی بزرگتر از 5 است ، که بالاترین حد دوستانی بود که می توان به آن اختصاص داد. مقدار "9" متغیر است و می تواند/باید زمانی تغییر کرد که "mostFriendsPersonCanHave" بزرگتر از 9 باشد. سه خط آخر کد (به استثنای پایان) tempMatrix را به ردیف بعدی "allFriendsMatrix" اضافه می کند. سپس tempMatrix را پاک می کند و برای نفر بعدی حساب می شود.
خروجی
این خروجی برای اولین بار در حلقه for (قبل از سه خط آخر) باید به نظر برسد.
tempMatrix = 16 8 17 16 13 NaN NaN NaN NaN
allFriendsMatrix =
16 8 17 16 13 NaN NaN NaN NaN NaN 8 8 2 7 11 NaN NaN NaN NaN 10 13 NaN NaN NaN NaN NaN NaN NaN NaN 11 17 2 NaN NaN NaN NaN NaN NaN 10 12 NaN NaN NaN NaN NaN NaN NaN NaN 4 13 2 12 NaN NaN NaN NaN NaN NaN 17 10 9 3 1 NaN NaN NaN NaN Na 16 16 6 NaN NaN NaN NaN NaN NaN 3 8 17 17 14 NaN NaN NaN NaN 20 19 3 NaN NaN NaN NaN NaN NaN NaN 13 10 NaN NaN NaN NaN NaN NaN NaN 2N 18 10 16 NaN NaN NaN NaN NaN NaN 2 6 14 3 13 NaN NaN NaN NaN NaN 8 16 14 8 NaN NaN NaN NaN NaN NaN 7 7 NaN NaN NaN NaN NaN NaN NaN 19 10 9 NaN NaN NaN NaN NaN NaN NaN 10 19 NaN NaN NaN NaN NaN NaN NaN NaN 5 18 NaN NaN NaN NaN NaN NaN NaN 1NaN NaN NaN NaN NaN NaN NaN NaN 16 7 13 10 1 NaN NaN NaN NaN
بعد ، این روابط را به adjMatrix اضافه کنید.
برای هر ردیف = 1: NUMOFPEOPLE
برای eachCol = 1: 9 if isnan (allFriendsMatrix (eachRow، eachCol)) == 0 adjMatrix (eachRow، allFriendsMatrix (eachRow ، eachCol)) = 1 ؛ adjMatrix (allFriendsMatrix (eachRow ، eachCol) ، eachRow) = 1 ؛ پایان پایان پایان
توضیح کد
این حلقه دوگانه برای هر سطر و ستون "allFriendsMatrix" می رود. دستور if برای همه مقادیری که "NaN" نیستند اجرا می شود. اساساً لبه ها یا خطوط نمودار را ایجاد می کند. بنابراین اولین خطی که ایجاد می شود شخص 1 به شخص 16 و نفر 16 به شخص 1 است. زیرا جهت دار نیست ، 1 باید برای هر دو تغییر کند! ما فقط نمی توانیم لبه 1 تا 16 را داشته باشیم و نه 16 به 1. آنها باید متقارن باشند تا در Matlab به درستی اجرا شود.
در شبیه سازی خود ، ما دریافتیم که مردم نمی توانند با خود ارتباط برقرار کنند. وقتی مقادیر را تصادفی می کنیم ، این احتمال وجود دارد که ماتریس مجاور ما این خطاها را داشته باشد.
بیایید این را با کد زیر برطرف کنیم:
برای هر = 1: NUMOFPEOPLE
adjMatrix (هر کدام ، هر کدام) = 0 ؛ پایان
توضیح کد
این حلقه برای اطمینان حاصل می کند که شخص 1 به شخص 1 متصل نیست ، شخص 2 به شخص 2 و غیره متصل نیست و همه آنها 0 باشد. همانطور که در قسمت خروجی در زیر مشاهده می کنید ، ما قطر مربع را داریم ماتریس از بالا سمت چپ به پایین راست همه 0 هستند.
خروجی
این adjMatrix نهایی برای شبیه سازی فعلی است. این شامل تمام خطوط موجود در نمودار است (شکل 2).
adjMatrix =
0 0 0 0 0 0 1 1 0 0 0 0 1 0 0 1 1 0 1 1 0 0 0 1 0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 1 0 0 0 0 1 0 1 0 1 1 1 1 0 0 0 1 0 0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 1 0 1 1 0 0 0 0 0 1 0 1 0 1 0 0 0 1 1 0 0 0 1 1 0 1 1 0 1 0 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 1 0 1 0 1 0 0 0 0 1 1 1 0 0 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0 0
برای مشاهده نمودار "adjMatrix" به شکل 2 مراجعه کنید.
مرحله 3: آمار بیماری ها را اضافه کنید
اکنون که برنامه شما می تواند یک نمودار با مجموعه ای از افراد تصادفی ایجاد کرده و روابط تصادفی ایجاد کند ، ما باید اطلاعات یا آمار بیماری را وارد کنیم تا ببینیم چگونه این تعاملات در یک جمعیت می تواند عفونت را افزایش یا کاهش دهد.
این متغیرها را ایجاد کنید:
unvacc٪ type: double؛ درصد احتمال عدم ابتلای افراد واکسینه نشده به این بیماری وجود دارد
نوع واکس٪: double؛ درصد احتمال عدم ابتلای افراد واکسینه به بیماری unvacc_perc٪ type: double؛ درصد جمعیت واکسینه نشده init_infect٪ type: int؛ درصد جمعیت واکسینه شده اند
در مرحله بعد باید برخی محاسبات را انجام دهیم.
ما قصد داریم یک "عفونت مات" ایجاد کنیم که یک ماتریس 3*NUMOFPEOPLE است.
vac_perc = 1-unvacc_perc؛
infeMat = nan (3 ، NUMOFPEOPLE) ؛ تعداد = دور (vacc_perc * NUMOFPEOPLE) ؛ infeMat (1 ، 1: number) = vacc؛ infeMat (1 ، شماره+1: پایان) = unvacc ؛ infeMat (2 ، 1: پایان) = 0 ؛ infeMat (2 ، 1: init_infect) = 1 ؛
توضیح کد
خط 1: درصد جمعیت واکسینه نشده محاسبه شده است
خط 2: ایجاد یک ماتریس 3*N از تعداد افراد
خط 3: تعداد افراد واکسینه شده را از درصد واکسینه کنید
خط 4: برای افراد واکسینه شده ، ایمنی مربوط به داشتن واکسن را به آنها بدهید. این مقدار بر اساس تحقیقات انجام شده در مورد این بیماری تعیین می شود.
خط 5: برای بقیه مردم (افراد واکسینه نشده) درصد مصونیت را به آنها بدهید. این مقدار بر اساس تحقیقات انجام شده در مورد این بیماری تعیین می شود.
خط 6: ابتدا همه افراد را طوری تنظیم کنید که آلوده نباشند.
خط 7: برای تعداد افرادی که در ابتدا آلوده شده اند ، مطابق آن اولین ستون زوج را پر کنید.
اکنون که همه پارامترهای شبیه سازی بیماری را تنظیم کرده ایم ، احتمال عفونت فرد (اعم از واکسینه و بدون واکسیناسیون) را تصادفی می کنیم. این کار در مرحله بعد با اختصاص مقادیر تصادفی بین 0 تا 1 به هر فرد در ردیف سوم این "infeMat" انجام می شود.
مرحله 4: احتمال اینکه فرد واکسینه و غیر واکسینه آلوده شود را تصادفی کنید
در مرحله بعد ، به هر فرد یک شماره تصادفی اختصاص دهید ، بعداً از آن برای تعیین اینکه آیا فرد مبتلا می شود یا نه استفاده می شود.
برای w = 1: طول (عفونت مات)
infeMat (3 ، w) = rand ؛ پایان
توضیح کد
این حلقه for مربوط به ردیف سوم "infeMat" است که در آخرین مرحله ایجاد شده است. 'rand' به هر شاخص ردیف 3 مقداری بین 0 تا 1 اختصاص می دهد.
خروجی
infeMat در حال حاضر کامل است! این مورد با جمعیت 100٪ واکسیناسیون و 1 نفر در ابتدا آلوده بود.
infeMat =
ستونهای 1 تا 12 0.7500 0.7500 0 0 0 0 0 0 0 0 0 0.0480 0.3593 0.2958 0.6291 0.1362 0.3740 0.8648 0.2503 0.2503
ردیف 1: درصد احتمال عدم ابتلا به این بیماری
ردیف 2: آلوده یا آلوده نشده (مقدار بولی)
ردیف 3: شماره مورد استفاده برای بررسی اینکه آیا فردی که آلوده نیست در صورت ملاقات با فرد آلوده مبتلا می شود یا خیر. اگر فرد آلوده با فرد آلوده ملاقات کند ، این تعداد بیشتر از شماره ردیف 1 (برای همان ستون) است ، پس آلوده هستند. ما این قابلیت را در مرحله 7 کدگذاری می کنیم.
مرحله 5: ایجاد ماتریس از افرادی که از اطلاعات اولیه واکسینه نشده اند و آلوده شده اند
2 ماتریس به نام های "matrixUnvacc" و "matrixInfected" ایجاد کنید که همه افراد آلوده را از infeMat ذخیره می کند. از این روش استفاده می شود تا بتوانیم نمودار افرادی را که آلوده ، واکسینه نشده یا واکسینه شده اند رنگ آمیزی کنیم ، و به تجسم تأثیر افراد واکسینه نشده در مقابل افراد واکسینه شده کمک کنیم.
هر کدام را پاک کنید
matrixInfected = ؛ matrixUnvacc = ؛ برای h = 1: length (infecMat) if infecMat (1، h) == unvacc پایان نهایی برای شخص = 1: NUMOFPEOPLE if infeMat (2 ، شخص) == 1 matrixInfected = [matrixInfected، person]؛ پایان پایان
توضیح کد
دو ماتریس خالی ایجاد کنید تا به ترتیب تعداد افرادی که واکسینه نشده و آلوده شده اند ذخیره شود. هر دو برای حلقه ها 20 بار اجرا می شوند و اگر دستور if راضی باشد ، عدد به ماتریس صحیح اضافه می شود.
خروجی
matrixUnvacc =
matrixInfected =
[1]
مرحله 6: رسم نمودار اولیه

در مرحله بعد ماتریس مجاورت را ترسیم می کنیم.
g = نمودار (adjMatrix) ؛
شکل (1) p = نمودار (g ، 'NodeColor' ، 'b' ، 'MarkerSize' ، 7) ؛ highlight (p، matrixUnvacc، 'NodeColor'، 'g') highlight (p، matrixInfected، 'NodeColor'، 'r') title_unvacc = unvacc_perc*100؛ title (['درصد افراد واکسینه نشده:' ، num2str (title_unvacc) ، '٪'])؛ مکث (سرعت)
توضیح کد
نظریه گراف در متلب دارای توابع است. وقتی از تابع graph () استفاده می کنیم ، می توانیم "adjMatrix" را به یک گراف واقعی جهت دار تبدیل کنیم. سپس باید با استفاده از تابع () plot یک نمودار ایجاد کنیم تا در واقع ظاهر آن را ببینیم. ما این نمودار () را روی یک متغیر قرار می دهیم تا بتوانیم در طول شبیه سازی راحت تر رنگ طرح را تغییر داده و تغییر دهیم. همه افراد (یا گره ها) در ابتدا روی رنگ "آبی" تنظیم شده اند. در مرحله بعد ، همه افراد واکسینه نشده روی رنگ "سبز" تنظیم شده اند. سپس افراد آلوده روی رنگ "قرمز" تنظیم می شوند. عنوان با توجه به درصد معینی از افراد واکسینه نشده مورد آزمایش تعیین می شود. تابع pause () اجرای MatLab را موقتاً متوقف می کند. ما از سرعت متغیری که پخش می شود عبور می کنیم که در ثانیه محاسبه می شود.
برای مشاهده نمودار تصادفی با کد رنگی به تصویر (بالا) مراجعه کنید.
در مورد تابع highlight () در MatLab بیشتر بیاموزید.
مرحله 7: پیشرفت عفونت را شبیه سازی کنید
در مرحله بعد ما باید بفهمیم چه کسی بعد از فعل و انفعالات (ثبت شده در adjMatrix) آلوده می شود و هنگامی که فردی آلوده می شود نمودار را به روز می کنیم.
از adjMatrix برای تعیین افرادی که پس از تعامل با افراد در یک روز آلوده شده اند استفاده کنید.
برای هر Row = 1: length (adjMatrix)
if infecMat (2 ، هر ردیف) == 1 برای هرCol = 1: length (adjMatrix) اگر adjMatrix (eachRow ، eachCol) == 1٪ eachRow = شخص٪ eachCol = دوستش٪ دوست هر شخص و ببینید آیا آلوده شده اند به if infecMat (3 ، هرCol)> عفونتMat (1 ، هرCol) برجسته (p ، eachCol ، 'NodeColor' ، 'r') مکث (سرعت) پایان پایان پایان پایان پایان
حلقه for برای هر فرد حلقه می کند. این بررسی می کند که اگر فرد مبتلا باشد ، هر یک از افراد/دوستانی که با آنها ارتباط داشته اند را بررسی می کند و بررسی می کند که آیا سطح ایمنی دوست بیشتر از قدرت بیماری است. اینجاست که "infeMat" که قبلاً ایجاد کرده بودیم مطرح می شود. ردیف 1 و 3 هر ستون از دوست مقایسه می شود و اگر ردیف 3 بزرگتر باشد ، به این معنی است که آن دوست از ایمنی کافی برای فرار از بیماری برخوردار نبوده و در نهایت آلوده می شود. در صورت آلوده شدن رنگ را با استفاده از highlight () به قرمز تغییر می دهیم.
حالا کد شما برای شبیه سازی باید کار کند! و برای هر اندازه جمعیت ، فقط NUMOFPEOPLE را تغییر دهید!
مرحله 8: از نظریه مونت کارلو استفاده کنید
برای این که یک قدم جلوتر برویم و داده ها را از شبیه ساز خود ('infeSim.m') استخراج کنیم ، می خواستیم روند درصد افراد واکسینه نشده و افراد واکسینه واکسینه شده را محاسبه و نمودار کنیم. ما فرض می کنیم که درصد افراد واکسینه شده آلوده باید بسیار کمتر از درصد افراد واکسینه نشده آلوده باشند.
مرحله 9: با شبیه سازی به یک تابع فایل ('infecim.m.m') را بسازید
برای اجرای مونت کارلو ، ما می خواهیم شبیه سازی را چندین بار اجرا کرده و داده ها را جمع آوری کنیم تا بتوانیم از آن برای ترسیم درصد افراد آلوده استفاده کنیم.
تابع را می توان به صورت زیر تنظیم کرد:
عملکرد خروجی = عفونت Sim (unvacc ، vac، NUMOFPEOPLE ، unvacc_perc ، init_infect ، سرعت)
متغیرهای شبیه سازی خود را کامنت کنید زیرا اکنون اینها را از طریق فایل اصلی منتقل می کنید (ما در مرحله 12 شروع به نوشتن این مطلب می کنیم):
unvacc ، vacc، NUMOFPEOPLE ، unvacc_perc ، init_infect
متغیر جدید
سرعت
در فایل اصلی (Monte_Carlo.m) اختصاص داده می شود.
توجه: برای خاتمه عملکرد ، انتهای قسمت پایین فایل تابع را فراموش نکنید!
مرحله 10: درصد افراد واکسینه نشده و واکسینه شده را که آلوده شده اند محاسبه کنید
این درصد افراد واکسینه نشده را که آلوده شده اند محاسبه می کند. این کد در انتهای فایل "infeSim.m" قرار می گیرد.
number_of_unvacc = 0؛
number_of_infec_unvacc = 0؛ ٪ درصد افراد واکسینه نشده را که برای x = 1 آلوده شده اند محاسبه می کند: length (infecMat) در صورت عفونت پایان دادن به عفونت MAT (1 ، x) == unvacc & پایان پایان ٪_of_unvacc_and_infec = (number_of_infec_unvacc / number_of_unvacc)*100 ؛
توضیح کد
در حلقه for ، بیش از NUMOPPEOPLE بار حلقه می شود. هر بار که تعداد عفونت در Mat مربوط به شماره واکسن نیست (یعنی 0.95 = 0.95 = 0.95) ، سپس تعداد افراد واکسینه نشده 1 افزایش می یابد. هر بار که تعداد عفونت ها با شماره واکسن مطابقت دارد و آنها آلوده هستند ، تعداد افراد آلوده و واکسینه نشده 1 افزایش می یابد. آخرین خط ، تعداد افراد آلوده و واکسینه نشده را بر تعداد کل افراد واکسینه نشده تقسیم می کند. سپس درصد از این محاسبه می شود.
چالش:
سعی کنید درصد واکسیناسیون افرادی که مبتلا شده اند را محاسبه کنید! (نکته: بسیار شبیه به این کد بالا است ، با این حال برخی از متغیرها تغییر کرده و نام ها تنظیم می شوند.)
سپس درصد افراد آلوده بر اساس کل جمعیت محاسبه می شود:
pre_per_infect = cumsum (infeMat (2 ،:))؛
per_infect = (pre_per_infect (1 ، NUMOFPEOPLE)/NUMOFPEOPLE)*100 ؛
توضیح کد
مجموع تجمعی با استفاده از ردیف دوم infeMat محاسبه می شود ، که بسته به اینکه آیا فرد آلوده است یا نه ، 1 و 0 را ذخیره می کند.از آنجا که تابع () cumsum یک ماتریس را برمی گرداند ، ما آخرین مقدار را در ماتریس ('pre_per_infect (1، NUMOFPEOPLE)') می گیریم ، که باید مجموع واقعی همه مقادیر 'infeMat (2،:)' باشد. با تقسیم مجموع بر NUMOPPEOPLE و ضرب آن در 100 ، به درصد نهایی افراد آلوده در کل جمعیت می رسیم.
مرحله 11: یک متغیر خروجی در عملکرد خود ایجاد کنید "infeSim.m"
خروجی = [per_infect ، درصد_unvacc_and_infec ، درصد_vacc_and_infec] ؛
توضیح کد
این اطلاعات را در خروجی ذخیره کنید ، که پس از فراخوانی و اجرای عملکرد به اصلی (Monte_Carlo.m) ارسال می شود. این داده ها برای نشان دادن نقاط درصد افراد مبتلا به واکسن و بدون واکسیناسیون استفاده می شود.
عملکرد "infeSim.m" شما باید در حال حاضر انجام شود! با این حال ، اجرا نمی شود زیرا ما هنوز باید اصلی را بنویسیم!
مرحله 12: ایجاد منو برای دریافت شرایط اولیه شبیه سازی از کاربر
به یاد داشته باشید که چگونه متغیر را گفتیم
سرعت
ایجاد می شود و از طریق عملکرد اصلی عبور می کند؟ ما باید مقادیری را برای انتقال به تابع بدست آوریم. توجه داشته باشید ، ترتیب مقادیر هنگام فراخوانی تابع اهمیت دارد!
با درخواست از کاربر برای تایپ برخی از پاسخ ها در ترمینال شروع کنید.
> بیماری را انتخاب کنید. توجه داشته باشید که به حروف بزرگ حساس است >> سیاه سرفه >> آنفولانزا >> سرخک >> بیماری انتخاب شده: آنفولانزا >> اندازه جمعیت را انتخاب کنید. >> 20 >> 200 >> جمعیت انتخاب شده: 20 >> سرعت شبیه سازی را انتخاب کنید. >> سریع >> آهسته >> سرعت انتخاب شده: سریع
این کد زیر از کاربر می پرسد که می خواهد چه بیماری را بررسی کند.
disp ("بیماری را انتخاب کنید. توجه داشته باشید که حساس به حروف است")
fprintf ('Pertussis / nFlu / n سرخک / n') بیماری = ورودی ('بیماری انتخاب شده' ، 's') ؛ اگر isequal (بیماری ، 'سیاه سرفه') واکسن = 0.85 ؛ ٪ 15 درصد شانس ابتلا به بیماری unvacc =.20؛ ٪ 80 درصد احتمال ابتلا به بیماری در غیر این صورت (بیماری ، "آنفولانزا") واکسن = 0.75 ؛ ٪ 25 درصد شانس ابتلا به بیماری unvacc =.31؛ ٪ 69 درصد احتمال ابتلا به بیماری در غیر این صورت (بیماری ، سرخک) واکسن =.97 ؛ ٪ 3 درصد شانس ابتلا به بیماری بدون واکسن =.10؛ ٪ 90 درصد احتمال پایان یافتن بیماری
توضیح کد:
تابع disp () دستور را روی صفحه چاپ می کند و همچنین گزینه های مختلف را چاپ می کند. بر این اساس بیماری تعیین می شود. این نسخه در حال حاضر ورودی نامعتبر را در نظر نمی گیرد. ورودی نامعتبر خطایی ایجاد می کند و برنامه را به طور کامل متوقف می کند. هر بیماری دارای مقادیر واکسن و واکسن مرتبط با آن است. این مقادیر تصادفی نیستند این مقادیر را از طریق تحقیق در مورد آمار بیماری ها بدست آوردیم.
در مرحله بعد ، ما باید از کاربر بپرسیم آیا می خواهد اندازه جمعیت بزرگ یا کوچک را برای بیماری انتخابی خود آزمایش کند.
disp ("انتخاب اندازه جمعیت.")
fprintf ('20 / n200 / n ') speed = input (' جمعیت انتخاب شده: '،' s ')؛ اگر نابرابر باشد (سرعت ، '20') اندازه_جمعیت = 20 ؛ elseif isequal (سرعت ، '200') اندازه_جمعیت = 200 ؛ پایان
توضیح کد
این یک بیانیه برای کاربر چاپ می کند و از کاربر می خواهد که چه اندازه جمعیتی را که می خواهد آزمایش کند وارد کند. این نسخه در حال حاضر ورودی نامعتبر را در نظر نمی گیرد. ورودی نامعتبر خطایی ایجاد می کند و برنامه را به طور کامل متوقف می کند. 20 مورد انتخاب شد زیرا اندازه نمونه کوچکی است که هنوز ایده خوبی از نحوه انتشار عفونت در جمعیت کمی نشان می دهد. 200 نفر به عنوان گزینه بزرگتر انتخاب شدند زیرا 200 نقطه ترسیم شده روی نمودار تقریباً هیچ نقطه ای را با هم تداخل نداشت ، بنابراین همه چیز به راحتی قابل مشاهده و از یکدیگر متمایز می شد.
در مرحله بعد ، ما باید سرعت شبیه سازی را پیدا کنیم.
disp ('انتخاب سرعت شبیه سازی.')
fprintf ('سریع / n آهسته / n') سرعت = ورودی ('سرعت انتخاب شده:' ، 's') ؛ اگر isequal (سرعت ، 'سریع') sim_speed = 0 ؛ elseif isequal (سرعت ، 'آهسته') sim_speed = 0.25 ؛ پایان
توضیح کد
این فرایند همانند گرفتن نوع بیماری و اندازه جمعیت بود. برای سریع ، هیچ وقفه ای وجود نخواهد داشت. و برای کند ، هنگام اجرای شبیه سازی 0.25 ثانیه در حلقه for وقفه ایجاد می شود.
عالی! اکنون ما تمام ورودی های کاربر مورد نیاز خود را داریم! بیایید به جمع آوری داده ها برای درصد های مختلف افراد واکسینه نشده بپردازیم.
مرحله 13: یک درصد افراد واکسینه نشده را انتخاب کرده و میانگین افراد واکسینه نشده و آلوده را به درصد انتخاب شده محاسبه کنید
این کد برای 0٪ افراد واکسینه نشده است.
٪ -------٪ 0 واکسینه نشده ------------
per_infect_av_0 = ؛ درصد_نواکس_و_اینفک_او_0 = ؛ برای i = 1:20 out = infeSim (unvacc ، vacc، اندازه_جمعیت ، 0 ، 1 ، sim_speed) ؛ per_infect_av_0 = [per_infect_av_0 ، خارج (1 ، 1)] ؛ درصد_نواکس_و_اینفك_او_0 = [درصد_نواكس_و_نفس_آو_0 ، خارج (1 ، 2)] ؛ پایان میانگین_فروش_0 = میانگین (per_infect_av_0) ؛ average_unvacc_and_infected_0 = میانگین (درصد_واونو_ک_و_اینفک_او_0) ؛
توضیح کد:
حلقه for 20 بار اجرا می شود. خروجی از تابع ، عفونت (Sim) در خارج ذخیره می شود. هر بار که حلقه for اجرا می شود ، درصد آلوده شدن در کل جمعیت به ماتریس "per_infect_av_0" اضافه می شود. علاوه بر این ، درصد افراد واکسینه نشده و آلوده نیز هر بار به ماتریس 'درصد_نواکس_ و_اینفک_او_0' اضافه می شود. در دو خط آخر ، این دو ماتریس فوق الذکر به طور میانگین و در متغیرها ذخیره می شوند. به طور خلاصه ، درصدها برای هر شبیه سازی ذخیره می شوند ، به طور میانگین و نمودار می شوند. مونت کارلو برای نشان دادن مقدار متوسط اجرای یک شبیه سازی و نمایش نتیجه استفاده می شود. برای اهداف تجربی خود ، ما انتخاب می کنیم که شبیه سازی 20 بار اجرا شود و این مقادیر را متوسط کنیم.
چالش:
برای درصد هایی که می خواهید آزمایش کنید ، این کار را تکرار کنید! این را می توان با تغییر نام متغیرها با توجه به درصد اعداد انجام داد. ما 0، ، 5، ، 10، ، 20، ، 30، و 50 tested آزمایش کردیم.
نکته:
تنها خطی که باید در کد واقعی تغییر کند این است
out = infeksim
صفر را به درصد به صورت اعشاری تغییر دهید. به عنوان مثال ، برای شبیه سازی 5٪ واکسینه نشده ، 0 باید با 0.5 جایگزین شود.
مرحله 14: نمودار: "روند عفونت در مقابل واکسینه نشده" واکسیناسیون بیماری خاص"
این کد برای ایجاد نمودار روند عفونت در افراد واکسینه نشده در مقابل افراد واکسینه نشده است.
graph_mat_y = [میانگین_فروشده_0 ، میانگین_فروشده_5 ، میانگین_عفونی_10 ، میانگین_عفونی_20 ، میانگین_عفونی_30 ، متوسط_آفتابی_50] ؛
graph_mat_x = [0 ، 5 ، 10 ، 20 ، 30 ، 50] ؛ شیب = (average_infected_5-average_infected_0)/5؛ line_y = [average_infected_0، (شیب*50)+average_infected_0]؛ line_x = [0، 50]؛ شکل (2) نمودار (graph_mat_x ، graph_mat_y) ؛ خط (line_x، line_y، 'Color'، 'red'، 'LineStyle'، '-')؛ عنوان (['روند عدم واکسیناسیون برای' ، بیماری])؛ xlabel ("درصد اولیه واکسینه نشده") ؛ ylabel ("درصد آلودگی نهایی")
توضیح کد
خط 1: مقدار y را به میانگین درصد آلوده اختصاص می دهد
خط 2: مقادیر x را به درصد درصد اولیه واکسینه نشده اختصاص می دهند
خط 3: محاسبه شیب 0 and و 5
خط 4: مقدار y خط را ذخیره کنید. این ادامه بخش 0 تا 5 درصد است.
خط 5: مقدار y را در خط ذخیره کنید. این خط طول نمودار را در بر می گیرد.
خط 6: ایجاد شکل
خط 7: مقادیر نمودار x و y درصد آلوده ، که واکسینه نشده اند را ترسیم کنید.
خط 8: خط را ترسیم کنید. این مورد نشان داده می شود که به صورت خطی افزایش نمی یابد ، بلکه به صورت نمایی افزایش می یابد.
خط 9: عنوان را برای نمودار تعیین کنید.
خط 10-11: برچسب x و y را برای نمودار تنظیم کنید.
اکنون باید بتوانید مشاهده کنید که درصد بیشتری از مردم واکسینه نشده ، میزان عفونت بیشتر است. همچنین خواهید دید که بیشتر نقاطی که قرمز می شوند ، نقاط سبز هستند که نشان می دهد واکسن تا حدی کمک می کند! امیدوارم از این آموزش خوشتان آمده باشد. اگر سوالی دارید کامنت کنید!
مرحله 15: محصول نهایی: شبیه سازی چگونه به نظر می رسد


تمام کد را می توانید در اینجا پیدا کنید
توصیه شده:
(بسیار ساده) مدل سازی بیماری (با استفاده از خراش): 5 مرحله

(بسیار ساده) مدل سازی بیماری (با استفاده از خراش): امروز ، ما شیوع بیماری را شبیه سازی می کنیم ، که شامل هر بیماری است ، نه لزوما COVID-19. این شبیه سازی از یک ویدیو توسط 3blue1brown الهام گرفته شده است ، که من به آن پیوند می دهم. از آنجا که این کار کشیدن و رها کردن است ، ما نمی توانیم تا آنجا که می توانیم با JS یا Pyt انجام دهیم
نمونه اولیه پروژه چراغ راهنمایی Atmega16 با استفاده از نمایش 7 بخش (شبیه سازی پروتئوس): 5 مرحله
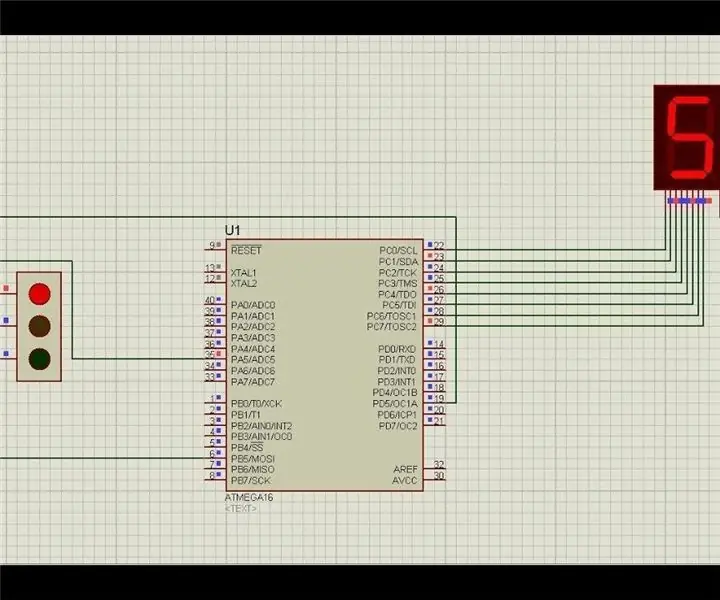
نمونه اولیه پروژه چراغ راهنمایی Atmega16 با استفاده از نمایش 7 بخش (شبیه سازی پروتئوس): در این پروژه ما قصد داریم پروژه چراغ راهنمایی بر اساس Atmega16 بسازیم. در اینجا ما یک قطعه 7 و 3 LED برای نشان دادن سیگنال های چراغ راهنمایی گرفته ایم
دکمه ایمنی بی سیم برای ایمنی PLC: 6 مرحله (همراه با تصاویر)

دکمه ایمنی بی سیم برای ایمنی PLC: این پروژه اثبات مفهوم من برای استفاده از IoT و (سرانجام) روباتیک برای ایجاد یک لایه ایمنی اضافی برای تأسیسات تولید خطرناک است. از این دکمه می توان برای شروع یا توقف چندین فرآیند ، از جمله کنترل سیگنال استفاده کرد
مشعل مجهز به USB! این پروژه می تواند از طریق پلاستیک / چوب / کاغذ بسوزد (پروژه سرگرم کننده همچنین باید چوبی بسیار ظریف باشد): 3 مرحله

مشعل مجهز به USB! این پروژه می تواند از طریق پلاستیک / چوب / کاغذ بسوزد (پروژه سرگرم کننده همچنین باید چوب بسیار ظریفی باشد): این USB را به کار نبرید !!!! از همه نظرات متوجه شدم که می تواند به رایانه شما آسیب برساند. کامپیوتر من خوب است از شارژر تلفن 600 ولت 5 ولت استفاده کنید. من از این استفاده کردم و خوب کار می کند و اگر از یک دوشاخه ایمنی برای قطع برق استفاده کنید ، هیچ چیزی آسیب نمی بیند
TECHNO VIKING! شاخ های LED در کلاه ایمنی فضایی وایکینگ: نشانگر حجم + کلاه ایمنی وایکینگ شفاف: 6 مرحله

TECHNO VIKING! شاخ های LED در کلاه ایمنی فضایی وایکینگ: شاخص حجم + کلاه وایکینگ شفاف: بله! این یک کلاه ایمنی برای وایکینگ های فضایی است. *** به روز رسانی ، این باید به کلاه تکنو وایکینگ تغییر نام دهد *** اما اکتبر 2010 است و من فقط امروز با تکنو وایکینگ آشنا شدم. خوب پشت منحنی میم. Whateva 'در اینجا او با محصولات بالاتر است
