فهرست مطالب:
- معرفی
- مرحله 1: شتاب سنج
- مرحله 2: ژیروسکوپ
- مرحله 3: ترکیب شتاب سنج و ژیروسکوپ
- همه چیز را با هم ترکیب کنید - ترکیب داده های شتاب سنج و ژیروسکوپ

تصویری: آموزش شتاب سنج و ژیروسکوپ: 3 مرحله

2024 نویسنده: John Day | [email protected]. آخرین اصلاح شده: 2024-01-30 08:59

معرفی
این راهنما برای همه علاقمندان به استفاده از شتاب سنج و ژیروسکوپ و همچنین دستگاه های ترکیبی IMU (واحد اندازه گیری اینرسیال) در پروژه های الکترونیکی آنها در نظر گرفته شده است.
ما پوشش خواهیم داد:
- شتاب سنج چه اندازه ای دارد؟
- ژیروسکوپ (یا ژیروسکوپ) چه اندازه ای دارد؟
- چگونه قرائت های آنالوگ را به دیجیتال (ADC) که از این سنسور دریافت می کنید به واحدهای فیزیکی تبدیل کنید (برای g برای شتاب سنج g ، برای ژیروسکوپ درجه سانتی گراد/ثانیه)
- نحوه ترکیب خواندن شتاب سنج و ژیروسکوپ به منظور دستیابی به اطلاعات دقیق در مورد تمایل دستگاه شما نسبت به سطح زمین
در طول مقاله سعی می کنم ریاضیات را به حداقل برسانم. اگر می دانید Sine/Cosine/Tangent چیست ، باید بتوانید این ایده ها را بدون توجه به پلتفرمی که استفاده می کنید درک کنید و از آنها در پروژه خود استفاده کنید: Arduino ، Propeller ، Basic Stamp ، تراشه های Atmel ، Microchip PIC و غیره.
افرادی هستند که معتقدند برای استفاده از واحد IMU به ریاضیات پیچیده نیاز دارید (فیلترهای پیچیده FIR یا IIR مانند فیلترهای کالمن ، فیلترهای پارک-مک کللان و غیره). می توانید در مورد همه آنها تحقیق کنید و به نتایج شگفت انگیز اما پیچیده ای برسید. روش من برای توضیح چیزها فقط به ریاضیات اولیه نیاز دارد. من به سادگی بسیار اعتقاد دارم. من فکر می کنم سیستمی که ساده باشد کنترل و نظارت بر آن آسان تر است ، علاوه بر این بسیاری از دستگاه های تعبیه شده قدرت و منابع لازم را برای پیاده سازی الگوریتم های پیچیده ای که نیاز به محاسبات ماتریسی دارند ، ندارند.
من به عنوان نمونه از واحد IMU جدید ، Acc_Gyro Accelerometer + Gyro IMU استفاده می کنم. در مثالهای زیر از پارامترهای این دستگاه استفاده خواهیم کرد. این دستگاه برای شروع یک دستگاه خوب است زیرا شامل 2 دستگاه است:
- LIS331AL (برگه اطلاعات) - شتاب سنج 2G سه محوری - LPR550AL (برگه اطلاعات) - پیچ و رول دو محوره ، ژیروسکوپ 500 درجه در ثانیه
آنها با هم یک واحد اندازه گیری اینرسی آزادی 5 درجه را نشان می دهند. حالا این اسم فانتزی است! با این وجود ، در پشت نام فانتزی یک دستگاه ترکیبی بسیار مفید وجود دارد که ما در این راهنما به طور مفصل به آن می پردازیم و توضیح می دهیم.
مرحله 1: شتاب سنج

برای درک این واحد ، ما با شتاب سنج شروع می کنیم. وقتی به شتاب سنج ها فکر می کنید ، اغلب تصویری از یک جعبه به شکل یک مکعب با یک توپ در داخل مفید است. شما ممکن است چیز دیگری مانند کوکی یا دونات را تصور کنید ، اما من یک توپ را تصور می کنم:

اگر ما این جعبه را در مکانی بدون میدان گرانشی یا در مورد آن بدون هیچ میدان دیگری که ممکن است بر موقعیت توپ تأثیر بگذارد ببریم - توپ به سادگی در وسط جعبه شناور می شود. می توانید تصور کنید که این جعبه در فضا بسیار دور از اجسام کیهانی قرار دارد ، یا اگر چنین مکانی به سختی یافت می شود ، حداقل یک فضاپیما در حال گردش در اطراف سیاره است که همه چیز در حالت بی وزن است. از تصویر بالا می بینید که ما به هر محور یک جفت دیوار اختصاص می دهیم (دیوار Y+ را برداشته ایم تا بتوانیم داخل کادر را نگاه کنیم). تصور کنید که هر دیوار به فشار حساس است. اگر جعبه را ناگهان به سمت چپ حرکت دهیم (آن را با شتاب 1g = 9.8m/s^2 شتاب می دهیم) ، توپ به دیوار X- برخورد می کند. سپس نیروی فشاری که توپ به دیوار وارد می کند را اندازه گیری می کنیم و مقدار 1 گرم را در محور X خروجی می دهیم.

لطفاً توجه داشته باشید که شتاب سنج در واقع نیرویی را تشخیص می دهد که در جهت مخالف بردار شتاب قرار دارد. این نیرو را اغلب نیروی اینرسی یا نیروی ساختگی می نامند. نکته ای که باید از آن یاد بگیرید این است که شتاب سنج شتاب را به صورت غیرمستقیم از طریق نیرویی که به یکی از دیواره های آن وارد می شود ، اندازه گیری می کند (طبق مدل ما ، ممکن است یک فنر یا چیز دیگری در شتاب سنج های واقعی باشد). این نیرو می تواند ناشی از شتاب باشد ، اما همانطور که در مثال بعدی خواهیم دید ، همیشه ناشی از شتاب نیست.
اگر ما مدل خود را برداریم و روی زمین بگذاریم ، توپ روی دیوار Z سقوط می کند و یک نیروی 1 گرم بر دیوار زیرین اعمال می کند ، همانطور که در تصویر زیر نشان داده شده است:

در این حالت جعبه حرکت نمی کند ، اما ما همچنان مقدار -1g را در محور Z می بینیم. فشاری که توپ به دیوار وارد کرده است توسط نیروی گرانش ایجاد شده است. از نظر تئوری ، ممکن است نیروی متفاوتی باشد - برای مثال ، اگر تصور کنید که توپ ما فلزی است ، قرار دادن آهنربا در کنار جعبه می تواند توپ را حرکت دهد تا به دیوار دیگری برخورد کند. این فقط برای اثبات این است که در اصل شتاب سنج نیرو را اندازه گیری می کند نه شتاب. فقط اتفاق می افتد که شتاب باعث ایجاد نیروی اینرسی می شود که توسط مکانیسم تشخیص نیروی شتاب سنج جذب می شود.
در حالی که این مدل دقیقاً نحوه ساخت سنسور MEMS نیست ، اغلب در حل مشکلات مربوط به شتاب سنج مفید است. در واقع سنسورهای مشابهی وجود دارند که دارای توپ های فلزی در داخل هستند ، به آنها سوئیچ شیب می گویند ، اما آنها اولیه هستند و معمولاً فقط می توانند تشخیص دهند که دستگاه در محدوده ای متمایل است یا خیر ، نه میزان تمایل.
تا کنون ما خروجی شتاب سنج را در یک محور واحد تجزیه و تحلیل کرده ایم و این تنها چیزی است که با شتاب سنج های یک محور بدست می آورید. ارزش واقعی شتاب سنج های سه محوری از این واقعیت ناشی می شود که آنها می توانند نیروهای اینرسی را در هر سه محور تشخیص دهند. بیایید به مدل جعبه خود بازگردیم و جعبه را 45 درجه به راست بچرخانیم. توپ در حال حاضر 2 دیوار را لمس می کند: Z- و X- همانطور که در تصویر زیر نشان داده شده است:

مقادیر 0.71 دلخواه نیستند ، در واقع تقریبی برای SQRT (1/2) هستند. این امر با معرفی مدل بعدی ما برای شتاب سنج روشن تر می شود.
در مدل قبلی ما نیروی گرانش را ثابت کرده و جعبه خیالی خود را چرخانده ایم. در 2 مثال آخر ما خروجی را در 2 موقعیت مختلف جعبه تحلیل کرده ایم ، در حالی که بردار نیرو ثابت مانده است. اگرچه این برای درک نحوه تعامل شتاب سنج با نیروهای خارجی مفید بود ، اما اگر سیستم مختصات را بر محورهای شتاب سنج ثابت کنیم و تصور کنیم که بردار نیرو به دور ما می چرخد ، انجام محاسبات عملی تر است.

لطفاً به مدل بالا نگاهی بیندازید ، من رنگ محورها را حفظ کردم تا بتوانید از مدل قبلی به مدل جدید انتقال ذهنی داشته باشید. فقط تصور کنید که هر محور در مدل جدید عمود بر چهره های مربوط به جعبه در مدل قبلی است. بردار R بردار نیرویی است که شتاب سنج اندازه گیری می کند (می تواند نیروی گرانشی یا نیروی اینرسی مثالهای بالا باشد یا ترکیبی از هر دو). Rx ، Ry ، Rz طرح بردار R در محورهای X ، Y ، Z هستند. لطفاً به رابطه زیر توجه کنید:
R^2 = Rx^2 + Ry^2 + Rz^2 (معادل 1)
که اساساً معادل قضیه فیثاغورث در سه بعدی است.
به یاد داشته باشید که کمی قبلتر به شما گفتم که مقادیر SQRT (1/2) 7 0.71 تصادفی نیست. اگر آنها را در فرمول بالا وصل کنید ، پس از به خاطر آوردن اینکه نیروی گرانش ما 1 گرم بود ، می توانیم تأیید کنیم که:
1^2 = (-SQRT (1/2))^2 + 0^2 + (-SQRT (1/2))^2
به سادگی با جایگزینی R = 1 ، Rx = -SQRT (1/2) ، Ry = 0 ، Rz = -SQRT (1/2) در معادله 1
پس از یک مقدمه طولانی نظریه ، ما به شتاب سنج های واقعی نزدیک می شویم. مقادیر Rx ، Ry ، Rz در واقع به صورت خطی با مقادیری که شتاب سنج واقعی شما تولید می کند مرتبط است و می توانید برای انجام محاسبات مختلف از آنها استفاده کنید.
قبل از رسیدن به آنجا اجازه دهید کمی در مورد نحوه شتاب سنج این اطلاعات را به ما ارائه دهیم. اکثر شتاب سنج ها در دو دسته دیجیتالی و آنالوگ قرار می گیرند. شتاب سنج های دیجیتال با استفاده از یک پروتکل سریال مانند I2C ، SPI یا USART اطلاعاتی را در اختیار شما قرار می دهند ، در حالی که شتاب سنج های آنالوگ سطح ولتاژ را در محدوده ای از پیش تعیین شده که شما باید با استفاده از ماژول ADC (مبدل آنالوگ به دیجیتال) به مقدار دیجیتال تبدیل کنید ، تولید می کند. من جزئیات زیادی در مورد نحوه کار ADC نخواهم داد ، تا حدی به این دلیل که این موضوع بسیار گسترده است و تا حدی به این دلیل که از یک پلت فرم به دیگری متفاوت است. برخی از میکروکنترلرها دارای ماژول های ADC هستند که برخی از آنها برای انجام تبدیل ADC به اجزای خارجی نیاز دارند. مهم نیست که از چه نوع ماژول ADC استفاده می کنید ، در نهایت یک مقدار در محدوده خاصی به دست خواهید آورد. برای مثال یک ماژول ADC 10 بیتی مقداری در محدوده 0..1023 تولید می کند ، توجه داشته باشید که 1023 = 2^10 -1. یک ماژول ADC 12 بیتی مقداری در محدوده 0..4095 تولید می کند ، توجه داشته باشید که 4095 = 2^12-1.
بیایید با در نظر گرفتن یک مثال ساده به پیش برویم ، فرض کنید ماژول ADC 10bit ما مقادیر زیر را برای سه کانال شتاب سنج (محورها) به ما داده است:
AdcRx = 586 AdcRy = 630 AdcRz = 561
هر ماژول ADC دارای ولتاژ مرجع است ، فرض کنید در مثال ما 3.3V است. برای تبدیل مقدار adbit 10bit به ولتاژ از فرمول زیر استفاده می کنیم:
VoltsRx = AdcRx * Vref / 1023
یک نکته سریع در اینجا: که در ADC 8bit آخرین تقسیم کننده 255 = 2 ^ 8 -1 و برای ADC 12bit آخرین تقسیم کننده 4095 = 2 ^ 12 -1 خواهد بود.
با اعمال این فرمول در هر 3 کانال دریافت می کنیم:
VoltsRx = 586 * 3.3V / 1023 = 8 1.89V (همه نتایج را به 2 نقطه اعشار گرد می کنیم) VoltsRy = 630 * 3.3V / 1023 = ~ 2.03V ولت Rz = 561 * 3.3V / 1023 = 1.81 ~
هر شتاب سنج دارای سطح ولتاژ صفر گرم است ، می توانید آن را در مشخصات پیدا کنید ، این ولتاژی است که برابر با 0 گرم است. برای به دست آوردن مقدار ولتاژ امضا شده ، باید تغییر از این سطح را محاسبه کنیم. فرض کنید سطح ولتاژ 0g ما VzeroG = 1.65V است. ما تغییرات ولتاژ از ولتاژ صفر-g را به صورت زیر محاسبه می کنیم:
DeltaVoltsRx = 1.89V - 1.65V = 0.24V DeltaVoltsRy = 2.03V - 1.65V = 0.38V DeltaVoltsRz = 1.81V - 1.65V = 0.16V
ما در حال حاضر قرائت شتاب سنج خود را بر حسب ولت داریم ، هنوز در g (9.8 m/s^2) نیست ، برای انجام تبدیل نهایی ، حساسیت شتاب سنج را که معمولاً بر حسب mV/g بیان می شود اعمال می کنیم. اجازه دهید حساسیت ما = 478.5mV/g = 0.4785V/g باشد. مقادیر حساسیت را می توان در مشخصات شتاب سنج یافت. برای بدست آوردن مقادیر نیروی نهایی در g ما از فرمول زیر استفاده می کنیم:
Rx = DeltaVoltsRx / حساسیت
Rx = 0.24V / 0.4785V / g = 0.5 ~ 0.5g Ry = 0.38V / 0.4785V / g = 7 0.79g Rz = 0.16V / 0.4785V / g = 33 0.33g
البته ما می توانیم همه مراحل را در یک فرمول ترکیب کنیم ، اما من تمام مراحل را طی کردم تا روشن شود که چگونه از خواندن ADC به یک جزء بردار نیرو که در g بیان شده است می پردازید.
Rx = (AdcRx * Vref / 1023 - VzeroG) / حساسیت (معادل 2) Ry = (AdcRy * Vref / 1023 - VzeroG) / حساسیت Rz = (AdcRz * Vref / 1023 - VzeroG) / حساسیت
ما در حال حاضر هر 3 جزء را داریم که بردار نیروی اینرسی ما را تعیین می کنند ، اگر دستگاه تحت نیروی دیگری به غیر از گرانش قرار نگیرد ، می توان فرض کرد که این جهت بردار نیروی گرانش ما است. اگر می خواهید شیب دستگاه را نسبت به زمین محاسبه کنید ، می توانید زاویه بین این بردار و محور Z را محاسبه کنید. اگر شما نیز به جهت جهت محور متمایل هستید ، می توانید این نتیجه را به 2 جزء تقسیم کنید: تمایل بر محور X و Y که می تواند به عنوان زاویه بین بردار گرانش و محورهای X / Y محاسبه شود. اکنون که ما مقادیر Rx ، Ry و Rz را محاسبه کرده ایم ، محاسبه این زوایا بسیار ساده تر از آن چیزی است که تصور می کنید. بیایید به آخرین مدل شتاب سنج خود بازگردیم و نشانه های اضافی را انجام دهیم:

زوایای مورد علاقه ما زاویه های بین محورهای X ، Y ، Z و بردار نیروی R. ما این زاویه ها را Axr ، Ayr ، Azr تعریف می کنیم. شما می توانید از مثلث زاویه راست تشکیل شده توسط R و Rx متوجه شوید که:
cos (Axr) = Rx / R ، و به طور مشابه: cos (Ayr) = Ry / R cos (Azr) = Rz / R
ما می توانیم از معادله 1 کسر کنیم که R = SQRT (Rx^2 + Ry^2 + Rz^2).
اکنون می توانیم زوایای خود را با استفاده از تابع arccos () (تابع معکوس cos ()) پیدا کنیم:
Axr = arccos (Rx/R) Ayr = arccos (Ry/R) Azr = arccos (Rz/R)
ما راه زیادی را برای توضیح مدل شتاب سنج طی کرده ایم ، فقط برای رسیدن به این فرمول ها. بسته به برنامه های کاربردی شما ممکن است بخواهید از هر فرمول میانی که ما گرفته ایم استفاده کنید. ما همچنین مدل ژیروسکوپ را به زودی معرفی می کنیم و خواهیم دید که چگونه می توان داده های شتاب سنج و ژیروسکوپ را برای برآورد دقیق تر شیب با هم ترکیب کرد.
اما قبل از اینکه این کار را انجام دهیم ، بیایید برخی از علائم مفیدتر را انجام دهیم:
cosX = cos (Axr) = Rx / R cozy = cos (Ayr) = Ry / R cosZ = cos (Azr) = Rz / R
این سه گانه اغلب Direction Cosine نامیده می شود و اساساً بردار واحد (بردار با طول 1) را نشان می دهد که جهت آن بردار R ما است. به راحتی می توانید تأیید کنید که:
SQRT (cosX^2 + دنج^2 + cosZ^2) = 1
این یک ویژگی خوب است زیرا ما را از نظارت بر مدول (طول) بردار R معاف می کند. اغلب اوقات اگر ما فقط به جهت بردار اینرسی خود علاقه مند باشیم ، منطقی است که مدول آن را عادی کنیم تا محاسبات دیگر را ساده کنیم.
مرحله 2: ژیروسکوپ

ما قصد نداریم هیچ مدل معادل جعبه ای را برای ژیروسکوپ مانند شتاب سنج معرفی کنیم ، بلکه مستقیماً به سراغ مدل دوم شتاب سنج می رویم و نشان خواهیم داد که ژیروسکوپ با توجه به این مدل چه اندازه ای دارد.

هر کانال ژیروسکوپ چرخش حول یکی از محورها را اندازه گیری می کند. به عنوان مثال یک ژیروسکوپ دو محوره چرخش حول محور X و Y را (یا برخی ممکن است "درباره" بگویند) اندازه گیری می کند. برای بیان این چرخش در اعداد ، بیایید برخی از نمادها را انجام دهیم. ابتدا اجازه دهید تعریف کنیم:
Rxz - نمایش بردار نیروی اینرسی R در صفحه XZ Ryz - نمایش بردار نیروی اینرسی R در صفحه YZ است
از مثلث زاویه راست تشکیل شده توسط Rxz و Rz ، با استفاده از قضیه فیثاغورث به دست می آوریم:
Rxz^2 = Rx^2 + Rz^2 ، و به طور مشابه: Ryz^2 = Ry^2 + Rz^2
همچنین توجه داشته باشید که:
R^2 = Rxz^2 + Ry^2 ، این می تواند از معادلات معادله 1 و بالاتر گرفته شود ، یا می تواند از مثلث زاویه راست تشکیل شده توسط R و Ryz R^2 = Ryz^2 + Rx^2 مشتق شده باشد.
ما در این مقاله از این فرمول ها استفاده نمی کنیم اما توجه به رابطه بین همه مقادیر در مدل ما مفید است.
در عوض ما قصد داریم زاویه بین محور Z و Rxz ، بردارهای Ryz را به صورت زیر تعریف کنیم:
Axz - زاویه بین Rxz (طرح R در صفحه XZ) و محور Z Ayz - زاویه بین Ryz (طرح R در صفحه YZ) و محور Z است
اکنون به اندازه گیری ژیروسکوپ نزدیک می شویم. ژیروسکوپ میزان تغییرات زوایای تعریف شده در بالا را اندازه گیری می کند. به عبارت دیگر ، مقداری را تولید می کند که به طور خطی با میزان تغییر این زوایا مرتبط است. برای توضیح این امر فرض می کنیم که ما زاویه چرخش حول محور Y (که زاویه Axz خواهد بود) را در زمان t0 اندازه گیری کرده ایم و آن را Axz0 تعریف می کنیم ، سپس این زاویه را در زمان بعد t1 اندازه گیری کردیم و Axz1 بود. نرخ تغییر به شرح زیر محاسبه می شود:
RateAxz = (Axz1 - Axz0) / (t1 - t0).
اگر Axz را بر حسب درجه و زمان را در ثانیه بیان کنیم ، این مقدار بر حسب deg/s بیان می شود. این چیزی است که ژیروسکوپ اندازه گیری می کند.
در عمل ژیروسکوپ (مگر اینکه ژیروسکوپ دیجیتالی خاصی باشد) به ندرت مقداری را که بر حسب درجه بر ثانیه بیان می کند به شما می دهد. همانطور که برای شتاب سنج ، یک مقدار ADC دریافت خواهید کرد که باید با استفاده از یک فرمول مشابه معادله به deg/s تبدیل کنید. 2 که برای شتاب سنج تعریف کرده ایم. بیایید ADC را به فرمول تبدیل deg/s ژیروسکوپ معرفی کنیم (فرض می کنیم از یک ماژول ADC 10bit استفاده می کنیم ، برای ADC 8bit 1023 را با 255 جایگزین می کنیم ، برای ADbit 12bit ADC را برای 1023 با 4095 جایگزین می کنیم).
RateAxz = (AdcGyroXZ * Vref / 1023 - VzeroRate) / Sensitivity Eq.3 RateAyz = (AdcGyroYZ * Vref / 1023 - VzeroRate) / حساسیت
AdcGyroXZ ، AdcGyroYZ - از ماژول adc ما بدست می آیند و نشان دهنده کانال هایی هستند که چرخش برآمدگی بردار R را در XZ به ترتیب در صفحه های YZ اندازه گیری می کنند ، که معادل چرخش به ترتیب در محورهای Y و X است.
Vref - همان ولتاژ مرجع ADC است که ما در مثال زیر از VzeroRate از 3.3V استفاده می کنیم - ولتاژ نرخ صفر است ، به عبارت دیگر ولتاژی که ژیروسکوپ هنگام چرخش خارج می کند ، برای برد Acc_Gyro به عنوان مثال 1.23V (شما می توانید این مقادیر را در مشخصات پیدا کنید) حساسیت - یعنی حساسیت ژیروسکوپ شما در mV / (deg / s) که اغلب بصورت mV / deg / s نوشته می شود ، اساساً به شما می گوید که چند میلی ولت خواهد بود اگر سرعت چرخش را یک درجه بر ثانیه افزایش دهید ، خروجی ژیروسکوپ افزایش می یابد. حساسیت برد Acc_Gyro برای مثال 2mV/deg/s یا 0.002V/deg/s است
بیایید مثالی بزنیم ، فرض کنید ماژول ADC ما مقادیر زیر را بر می گرداند:
AdcGyroXZ = 571 AdcGyroXZ = 323
با استفاده از فرمول فوق ، و با استفاده از پارامترهای مشخصات برد Acc_Gyro ، موارد زیر را دریافت می کنیم:
RateAxz = (571 * 3.3V/1023 - 1.23V)/(0.002V/درجه/ثانیه) = 6 306 درجه سانتیگراد در ثانیه RateAyz = (323 * 3.3V/1023 - 1.23V)/(0.002V/درجه/ثانیه) = ~ -94 درجه در ثانیه
به عبارت دیگر ، دستگاه حول محور Y (یا می توانیم بگوییم در صفحه XZ می چرخد) با سرعت 306 درجه در ثانیه و حول محور X (یا می توانیم بگوییم در صفحه YZ می چرخد) با سرعت - می چرخد. 94 درجه در ثانیه لطفاً توجه داشته باشید که علامت منفی به این معنی است که دستگاه در جهت مخالف از جهت مثبت متعارف می چرخد. طبق قرارداد یک جهت چرخش مثبت است. یک برگه مشخصات ژیروسکوپ خوب به شما نشان می دهد که کدام جهت مثبت است ، در غیر این صورت باید با آزمایش روی دستگاه و ذکر اینکه جهت چرخش منجر به افزایش ولتاژ در پین خروجی می شود ، آن را پیدا کنید. بهتر است این کار را با استفاده از اسیلوسکوپ انجام دهید زیرا به محض توقف چرخش ، ولتاژ به سطح صفر کاهش می یابد. اگر از مولتی متر استفاده می کنید ، باید سرعت چرخش را حداقل برای چند ثانیه حفظ کرده و ولتاژ را در طول این چرخش یادداشت کنید ، سپس آن را با ولتاژ نرخ صفر مقایسه کنید. اگر بیشتر از ولتاژ نرخ صفر باشد به این معنی است که جهت چرخش مثبت است.
مرحله 3: ترکیب شتاب سنج و ژیروسکوپ

همه چیز را با هم ترکیب کنید - ترکیب داده های شتاب سنج و ژیروسکوپ
اگر این مقاله را می خوانید ، احتمالاً یک دستگاه IMU را خریداری کرده اید یا قصد خرید آن را دارید ، یا احتمالاً قصد دارید دستگاهی از دستگاه های شتاب سنج و ژیروسکوپ جداگانه بسازید.
اولین قدم در استفاده از دستگاه IMU ترکیبی که شتاب سنج و ژیروسکوپ را ترکیب می کند ، هماهنگ سازی سیستم های مختصات آنها است. ساده ترین راه برای انجام این کار این است که سیستم مختصات شتاب سنج را به عنوان سیستم مختصات مرجع خود انتخاب کنید. اکثر برگه های اطلاعات شتاب سنج جهت محورهای X ، Y ، Z را نسبت به تصویر تراشه یا دستگاه فیزیکی نشان می دهند. به عنوان مثال ، در اینجا جهت محورهای X ، Y ، Z همانطور که در مشخصات مربوط به صفحه Acc_Gyro نشان داده شده است ، آمده است:

مراحل بعدی عبارتند از:
خروجی های ژیروسکوپ را که مربوط به مقادیر RateAxz ، RateAyz در بالا است شناسایی کنید. تعیین کنید که آیا این خروجی ها به دلیل موقعیت فیزیکی ژیروسکوپ نسبت به شتاب سنج باید معکوس شوند
فرض نکنید که اگر یک ژیروسکوپ دارای خروجی با علامت X یا Y باشد ، با هر محور در سیستم مختصات شتاب سنج مطابقت دارد ، حتی اگر این خروجی بخشی از یک واحد IMU باشد. بهترین راه آزمایش آن است. با فرض اینکه شما موقعیت ژیروسکوپ را نسبت به شتاب سنج ثابت کرده اید. فرض بر این است که مرزهای ژیروسکوپ و شتاب سنج موازی یکدیگر هستند ، یعنی شما ژیروسکوپ را در زاویه ای چند برابر 90 درجه نسبت به تراشه شتاب سنج قرار می دهید. اگر یک هیئت مدیره IMU را خریداری کرده اید ، احتمال وجود دارد که آنها قبلاً به این ترتیب تراز شده باشند. ما در این مقاله قصد نداریم در مورد مدل هایی که ژیروسکوپ در مقایسه با شتاب سنج (فرض می کنیم 45 یا 30 درجه) در یک زاویه نامنظم قرار می گیرد ، بحث کنیم ، اگرچه ممکن است در برخی از کاربردها مفید باشد.
در اینجا یک توالی نمونه برای تعیین خروجی ژیروسکوپ با مقدار RateAxz که در بالا مورد بحث قرار گرفت ، آمده است.
- از قرار دادن دستگاه در موقعیت افقی شروع کنید. هر دو خروجی X و Y شتاب سنج می توانند ولتاژ صفر گرم را تولید کنند (برای مثال برای برد Acc_Gyro این 1.65 ولت است)
- شروع بعدی چرخاندن دستگاه حول محور Y ، راه دیگر این است که دستگاه را در صفحه XZ بچرخانید ، به این ترتیب خروجی های شتاب سنج X و Z تغییر کرده و خروجی Y ثابت می ماند. - هنگام چرخاندن دستگاه با سرعت ثابت که خروجی ژیروسکوپ تغییر می کند ، سایر خروجی های ژیروسکوپ باید ثابت بمانند - خروجی ژیروسکوپ که در حین چرخش حول محور Y تغییر می کند (چرخش در صفحه XZ) مقدار ورودی AdcGyroXZ را فراهم می کند ، که از آن ما RateAxz را محاسبه می کنیم - آخرین مرحله این است که مطمئن شوید جهت چرخش با مدل ما مطابقت دارد ، در برخی موارد ممکن است مجبور شوید مقدار RateAxz را به دلیل موقعیت فیزیکی ژیروسکوپ نسبت به شتاب سنج معکوس کنید - دوباره آزمایش فوق را انجام دهید ، دستگاه را به دور خود بچرخانید محور Y ، این بار خروجی X شتاب سنج را کنترل کنید (در مدل ما AdcRx). اگر AdcRx رشد کند (اولین 90 درجه چرخش از حالت افقی) ، AdcGyroXZ نیز باید رشد کند. در غیر این صورت باید RateAxz را معکوس کنید ، می توانید با وارد کردن یک علامت علامت در معادله 3 ، به این موارد دست یابید:
RateAxz = InvertAxz * (AdcGyroXZ * Vref / 1023 - VzeroRate) / حساسیت ، جایی که InvertAxz 1 یا -1 است
با چرخاندن دستگاه در اطراف محور X ، می توانید آزمایش مشابهی را برای RateAyz انجام دهید ، و می توانید تشخیص دهید که کدام خروجی ژیروسکوپ مربوط به RateAyz است و اگر باید معکوس شود. هنگامی که مقدار InvertAyz را بدست آوردید ، باید از فرمول زیر برای محاسبه RateAyz استفاده کنید:
RateAyz = InvertAyz * (AdcGyroYZ * Vref / 1023 - VzeroRate) / حساسیت
اگر این آزمایشات را روی تخته Acc_Gyro انجام دهید ، نتایج زیر را دریافت خواهید کرد:
- پین خروجی RateAxz GX4 و InvertAxz = -1 است. - پین خروجی RateAyz GY4 و InvertAyz = -1 است
از این به بعد ما در نظر می گیریم که شما IMU خود را به گونه ای تنظیم کرده اید که بتوانید مقادیر صحیح برای Axr ، Ayr ، Azr (همانطور که در قسمت 1 شتاب سنج تعریف شده است) و RateAxz ، RateAyz (همانطور که در قسمت 2. ژیروسکوپ تعریف شده است) محاسبه کنید.) در ادامه روابط بین این مقادیر را که برای به دست آوردن برآورد دقیق تر از شیب دستگاه نسبت به سطح زمین مفید است ، تجزیه و تحلیل می کنیم.
شاید در این مورد از خود بپرسید ، اگر مدل شتاب سنج زاویه های تمایل Axr ، Ayr ، Azr را به ما نشان داده است ، چرا ما می خواهیم با داده های ژیروسکوپ مزاحم شویم؟ پاسخ ساده است: همیشه نمی توان 100٪ به داده های شتاب سنج اعتماد کرد. دلایل مختلفی وجود دارد ، به یاد داشته باشید که شتاب سنج نیروی اینرسی را اندازه گیری می کند ، چنین نیرویی می تواند ناشی از گرانش (و در حالت ایده آل فقط گرانش) باشد ، اما ممکن است در اثر شتاب (حرکت) دستگاه نیز ایجاد شود. در نتیجه حتی اگر شتاب سنج در وضعیت نسبتاً پایداری باشد ، هنوز به ارتعاشات و به طور کلی سر و صدای مکانیکی بسیار حساس است. این دلیل اصلی این است که اکثر سیستم های IMU از ژیروسکوپ برای برطرف کردن خطاهای شتاب سنج استفاده می کنند. اما این چگونه انجام می شود؟ و آیا ژیروسکوپ عاری از سر و صدا است؟
ژیروسکوپ عاری از سر و صدا نیست ، زیرا چرخش را اندازه گیری می کند و نسبت به حرکات مکانیکی خطی حساسیت کمتری دارد ، نوع نویز شتاب سنج از آن رنج می برد ، اما ژیروسکوپ ها مشکلات دیگری مانند مثال رانش (عدم بازگشت به مقدار صفر) دارند. وقتی چرخش متوقف می شود). با این وجود با استفاده از میانگین داده هایی که از شتاب سنج و ژیروسکوپ به دست می آید ، می توانیم تخمین نسبتاً بهتری از شیب دستگاه فعلی نسبت به آنچه با استفاده از داده های شتاب سنج به تنهایی بدست می آوریم ، بدست آوریم.
در مراحل بعدی ، الگوریتمی را معرفی می کنم که از ایده های مورد استفاده در فیلتر کالمن الهام گرفته شده است ، اما اجرای آن در دستگاه های تعبیه شده بسیار ساده تر و آسان تر است. قبل از آن ابتدا ببینیم که می خواهیم الگوریتم ما چه چیزی را محاسبه کند. خوب ، این جهت بردار نیروی گرانشی R = [Rx، Ry، Rz] است که از آن می توان مقادیر دیگری مانند Axr ، Ayr ، Azr یا cosX ، cozy ، cosZ را بدست آورد که به ما ایده ای در مورد تمایل دستگاه ما می دهد در مورد سطح زمین ، ما در مورد رابطه بین این مقادیر در قسمت 1 بحث می کنیم. ممکن است بگوییم - آیا ما قبلاً این مقادیر Rx ، Ry ، Rz را از معادله 2 در قسمت 1 نداریم؟ خوب بله ، اما به یاد داشته باشید که این مقادیر فقط از داده های شتاب سنج گرفته شده اند ، بنابراین اگر بخواهید آنها را مستقیماً در برنامه خود استفاده کنید ، ممکن است سر و صدای بیشتری از آنچه برنامه شما تحمل می کند ، دریافت کنید. برای جلوگیری از سردرگمی بیشتر ، اجازه دهید اندازه گیری های شتاب سنج را به شرح زیر تعریف کنیم:
Racc - بردار نیروی اینرسی اندازه گیری شده توسط شتاب سنج است که از اجزای زیر تشکیل شده است (پیش بینی در محورهای X ، Y ، Z):
RxAcc = (AdcRx * Vref / 1023 - VzeroG) / حساسیت RyAcc = (AdcRy * Vref / 1023 - VzeroG) / حساسیت RzAcc = (AdcRz * Vref / 1023 - VzeroG) / حساسیت
تا کنون ما مجموعه ای از مقادیر اندازه گیری شده داریم که می توانیم به طور کامل از مقادیر ADC شتاب سنج بدست آوریم. ما این مجموعه داده را "بردار" می نامیم و از علامت زیر استفاده می کنیم.
Racc = [RxAcc ، RyAcc ، RzAcc]
از آنجا که این اجزای Racc را می توان از داده های شتاب سنج بدست آورد ، می توانیم آن را ورودی الگوریتم خود بدانیم.
لطفاً توجه داشته باشید که چون Racc نیروی گرانش را اندازه گیری می کند ، اگر فرض کنید که طول این بردار به شرح زیر مساوی یا نزدیک به 1 گرم است ، درست خواهید بود.
| Racc | = SQRT (RxAcc^2 + RyAcc^2 + RzAcc^2) ،
اما برای اطمینان از به روزرسانی این بردار منطقی است:
Racc (نرمال شده) = [RxAcc/| Racc | ، RyAcc/| Racc | ، RzAcc/| Racc |].
این امر باعث می شود که طول بردار Racc نرمال شده شما همیشه 1 باشد.
در مرحله بعد یک بردار جدید معرفی می کنیم و آن را صدا می کنیم
استراحت = [RxEst ، RyEst ، RzEst]
این خروجی الگوریتم ما خواهد بود ، این مقادیر تصحیح شده بر اساس داده های ژیروسکوپ و بر اساس داده های برآورد گذشته است.
در اینجا این است که الگوریتم ما چه کار خواهد کرد: ما یک بردار برآورد جدید Rest را خروجی می دهیم. - ما استراحت را "بهترین شرط بندی" ما در مورد موقعیت فعلی دستگاه می دانیم.
بیایید ببینیم چگونه می توانیم آن را کار کنیم.
دنباله خود را با اعتماد به شتاب سنج و تعیین موارد زیر شروع می کنیم:
استراحت (0) = Racc (0)
به یاد داشته باشید Rest و Racc بردار هستند ، بنابراین معادله فوق فقط یک راه ساده برای نوشتن 3 مجموعه معادله و جلوگیری از تکرار است:
RxEst (0) = RxAcc (0) RyEst (0) = RyAcc (0) RzEst (0) = RzAcc (0)
در مرحله بعد ، اندازه گیری های منظم را در فواصل زمانی برابر T ثانیه انجام می دهیم و اندازه گیری های جدیدی را به دست می آوریم که آنها را Racc (1) ، Racc (2) ، Racc (3) و غیره تعریف می کنیم. ما همچنین برآوردهای جدیدی را در هر بازه زمانی استراحت (1) ، استراحت (2) ، استراحت (3) و غیره صادر می کنیم.
فرض کنید ما در مرحله n هستیم. ما دو مجموعه ارزش شناخته شده داریم که می خواهیم از آنها استفاده کنیم:
استراحت (n -1) - برآورد قبلی ما ، با Rest (0) = Racc (0) Racc (n) - اندازه گیری شتاب سنج فعلی ما
قبل از محاسبه Rest (n) ، بیایید مقدار اندازه گیری شده جدیدی را معرفی کنیم که می توانیم از ژیروسکوپ و برآورد قبلی بدست آوریم.
ما آن را Rgyro می نامیم ، و همچنین بردار متشکل از 3 جزء است:
Rgyro = [RxGyro ، RyGyro ، RzGyro]
ما این بردار را یک به یک محاسبه می کنیم. ما با RxGyro شروع می کنیم.

بیایید با مشاهده رابطه زیر در مدل ژیروسکوپ خود شروع کنیم ، از مثلث زاویه راست تشکیل شده توسط Rz و Rxz می توان نتیجه گرفت:
tan (Axz) = Rx/Rz => Axz = atan2 (Rx، Rz)
Atan2 ممکن است تابعی باشد که قبلاً از آن استفاده نکرده اید ، شبیه atan است ، با این تفاوت که مقادیر (-PI، PI) را در مقابل (-PI/2، PI/2) که توسط atan بازگردانده می شود ، و طول می کشد 2 استدلال به جای یک. این به ما امکان می دهد دو مقدار Rx ، Rz را به زاویه در محدوده کامل 360 درجه (-PI به PI) تبدیل کنیم. می توانید در مورد atan2 اینجا بیشتر بخوانید.
بنابراین با دانستن RxEst (n-1) و RzEst (n-1) می توانیم موارد زیر را بیابیم:
Axz (n-1) = atan2 (RxEst (n-1) ، RzEst (n-1)).
به یاد داشته باشید که ژیروسکوپ میزان تغییر زاویه Axz را اندازه گیری می کند. بنابراین می توان زاویه جدید Axz (n) را به صورت زیر برآورد کرد:
Axz (n) = Axz (n-1) + نرخAxz (n) * T
به یاد داشته باشید که RateAxz را می توان از خواندن ADC ژیروسکوپ دریافت کرد. یک فرمول دقیق تر می تواند از نرخ چرخش متوسط به شرح زیر استفاده کند:
RateAxzAvg = (RateAxz (n) + RateAxz (n-1)) / 2 Axz (n) = Axz (n-1) + RateAxzAvg * T
به همان روشی که می توانیم پیدا کنیم:
Ayz (n) = Ayz (n-1) + RateAyz (n) * T
خوب حالا Axz (n) و Ayz (n) داریم. از کجا می خواهیم RxGyro/RyGyro را کسر کنیم؟ از معادله 1 می توانیم طول بردار Rgyro را به صورت زیر بنویسیم:
| ریگرو | = SQRT (RxGyro^2 + RyGyro^2 + RzGyro^2)
همچنین به دلیل اینکه ما بردار Racc خود را عادی کردیم ، ممکن است فرض کنیم که طول آن 1 است و پس از چرخش تغییری نکرده است ، بنابراین نوشتن نسبتاً ایمن است:
| ریگرو | = 1
بیایید برای محاسبات زیر یک علامت کوتاه تر موقت اتخاذ کنیم:
x = RxGyro ، y = RyGyro ، z = RzGyro
با استفاده از روابط بالا می توانیم بنویسیم:
x = x / 1 = x / SQRT (x^2+y^2+z^2)
بیایید عدد و مخرج کسر را بر SQRT تقسیم کنیم (x^2 + z^2)
x = (x / SQRT (x^2 + z^2)) / SQRT ((x^2 + y^2 + z^2) / (x^2 + z^2))
توجه داشته باشید که x / SQRT (x^2 + z^2) = sin (Axz) ، بنابراین:
x = sin (Axz) / SQRT (1 + y^2 / (x^2 + z^2))
حال عدد و مخرج کسر داخل SQRT را در z^2 ضرب کنید
x = sin (Axz) / SQRT (1 + y^2 * z^2 / (z^2 * (x^2 + z^2)))
توجه داشته باشید که z / SQRT (x^2 + z^2) = cos (Axz) و y / z = tan (Ayz) ، بنابراین در نهایت:
x = sin (Axz) / SQRT (1 + cos (Axz)^2 * tan (Ayz)^2)
با بازگشت به علامت گذاری خود دریافت می کنیم:
RxGyro = sin (Axz (n)) / SQRT (1 + cos (Axz (n))^2 * tan (Ayz (n))^2)
به همین ترتیب ما آن را پیدا می کنیم
RyGyro = sin (Ayz (n)) / SQRT (1 + cos (Ayz (n))^2 * tan (Axz (n))^2)
اکنون ، سرانجام می توانیم پیدا کنیم:
RzGyro = علامت (RzGyro)*SQRT (1 - RxGyro^2 - RyGyro^2).
جایی که علامت (RzGyro) = 1 هنگام RzGyro> = 0 ، و علامت (RzGyro) = -1 هنگام RzGyro <0.
یک راه ساده برای برآورد این امر این است که:
علامت (RzGyro) = علامت (RzEst (n-1))
در عمل مراقب باشید وقتی RzEst (n-1) نزدیک به 0 است. در این حالت می توانید فاز ژیروسکوپ را به طور کامل رد کنید و تعیین کنید: Rgyro = استراحت (n-1). Rz به عنوان مرجعی برای محاسبه زوایای Axz و Ayz استفاده می شود و وقتی نزدیک به 0 باشد ، ممکن است مقادیر سرریز شده و نتایج بدی را ایجاد کند. شما در دامنه اعداد بزرگ نقاط شناور قرار خواهید گرفت که در آن پیاده سازی تابع tan () / atan () ممکن است فاقد دقت باشد.
بنابراین بیایید آنچه را که تا کنون داریم تجدید کنیم ، ما در مرحله n الگوریتم خود هستیم و مقادیر زیر را محاسبه کرده ایم:
Racc - خوانش های فعلی از شتاب سنج ما Rgyro - به دست آمده از Rest (n -1) و قرائت ژیروسکوپ فعلی
برای محاسبه برآورد به روز شده Rest (n) از کدام مقادیر استفاده می کنیم؟ احتمالاً حدس زده اید که ما از هر دو استفاده خواهیم کرد. ما از میانگین وزنی استفاده می کنیم ، به این صورت که:
استراحت (n) = (Racc * w1 + Rgyro * w2) / (w1 + w2)
ما می توانیم این فرمول را با تقسیم کردن متر و مخرج کسر بر w1 ساده کنیم.
استراحت (n) = (Racc * w1/w1 + Rgyro * w2/w1)/(w1/w1 + w2/w1)
و پس از جایگزینی w2/w1 = wGyro بدست می آوریم:
استراحت (n) = (Racc + Rgyro * wGyro) / (1 + wGyro)
در انجمن فوق wGyro به ما می گوید که ما در مقایسه با شتاب سنج خود به ژیروسکوپ خود چقدر اعتماد داریم. این مقدار را می توان به صورت تجربی انتخاب کرد معمولاً مقادیر بین 5..20 نتایج خوبی را به همراه خواهد داشت.
تفاوت اصلی این الگوریتم با فیلتر کالمن این است که این وزن نسبتاً ثابت است ، در حالی که در فیلتر کالمن وزن ها بر اساس سر و صدای اندازه گیری شده از شتاب سنج به طور دائم به روز می شوند. فیلتر کالمن بر ارائه "بهترین" نتایج نظری متمرکز است ، در حالی که این الگوریتم می تواند نتایج "به اندازه کافی خوب" را برای کاربرد عملی شما به شما ارائه دهد. شما می توانید یک الگوریتم را تنظیم کنید که wGyro را بسته به برخی از عوامل نویز که اندازه گیری می کنید تنظیم می کند ، اما مقادیر ثابت برای اکثر برنامه ها به خوبی کار می کند.
ما تا دریافت مقادیر برآورد به روز شده خود یک قدم فاصله داریم:
RxEst (n) = (RxAcc + RxGyro * wGyro) / (1 + wGyro) RyEst (n) = (RyAcc + RyGyro * wGyro) / (1 + wGyro) RzEst (n) = (RzAcc + RzGyro * wGyro) / (1 + wGyro)
حالا بیایید دوباره این بردار را عادی کنیم:
R = SQRT (RxEst (n)^2 + RyEst (n)^2 + RzEst (n)^2)
RxEst (n) = RxEst (n)/R RyEst (n) = RyEst (n)/R RzEst (n) = RzEst (n)/R
و ما آماده ایم که دوباره حلقه خود را تکرار کنیم.
این راهنما در ابتدا در starlino.com ظاهر شد ، من چند ویرایش سبک انجام دادم و مجدداً با اجازه آن را پست کردم. ممنون استارلینو!
توصیه شده:
MPU6050-شتاب سنج+حسگر ژیروسکوپ مبانی: 3 مرحله

MPU6050-شتاب سنج+حسگر ژیروسکوپ مبانی: MPU6050 یک سنسور بسیار مفید است. mpu 6050 یک IMU است: واحد اندازه گیری اینرسی (IMU) یک دستگاه الکترونیکی است که نیروی خاص بدن ، میزان زاویه ای و گاهی جهت گیری را اندازه گیری و گزارش می کند. بدن ، با استفاده از ترکیب
SmartPhone Game Simulator- بازی های ویندوز را با استفاده از Gesture Control IMU ، شتاب سنج ، ژیروسکوپ ، مغناطیس سنج انجام دهید: 5 مرحله
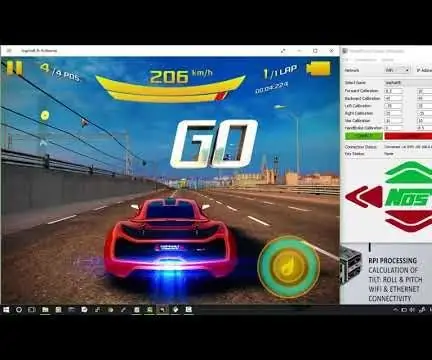
SmartPhone Game Simulator- با استفاده از Gesture Control IMU ، شتاب سنج ، ژیروسکوپ ، مغناطیس سنج بازی های ویندوز را اجرا کنید: از این پروژه پشتیبانی کنید: https://www.paypal.me/vslcreations با اهدا به کدهای منبع باز & amp؛ حمایت از توسعه بیشتر
Arduino Nano و Visuino: تبدیل شتاب به زاویه از شتاب سنج و ژیروسکوپ سنسور MPU6050 I2C: 8 مرحله (همراه با تصاویر)
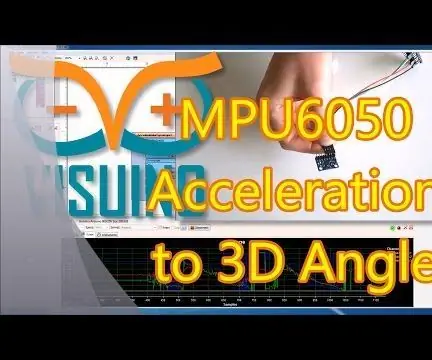
Arduino Nano و Visuino: تبدیل شتاب به زاویه از شتاب سنج و ژیروسکوپ سنسور MPU6050 I2C: چندی پیش من آموزشی را در مورد نحوه اتصال شتاب سنج MPU9250 ، ژیروسکوپ و سنسور قطب نما به آردوینو نانو و برنامه ریزی آن با Visuino برای ارسال داده ها و نمایش بسته ها ارسال کردم. آن را بر روی دامنه و ابزارهای بصری قرار می دهد. شتاب سنج X ، Y ،
آردوینو نانو: شتاب سنج ژیروسکوپ قطب نما MPU9250 I2C سنسور با Visuino: 11 مرحله
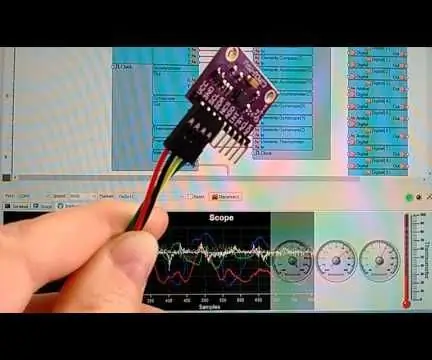
آردوینو نانو: شتاب سنج ژیروسکوپ قطب نما MPU9250 I2C Sensor With Visuino: MPU9250 یکی از پیشرفته ترین سنسورهای شتاب سنج ، ژیروسکوپ و قطب نما با اندازه کوچک است که در حال حاضر موجود است. آنها دارای بسیاری از ویژگی های پیشرفته هستند ، از جمله فیلترینگ کم گذر ، تشخیص حرکت و حتی یک پردازنده تخصصی قابل برنامه ریزی
اندازه گیری زاویه با استفاده از ژیروسکوپ ، شتاب سنج و آردوینو: 5 مرحله

اندازه گیری زاویه با استفاده از ژیروسکوپ ، شتاب سنج و آردوینو: این دستگاه نمونه اولیه ای از چیزی است که در نهایت به یک ربات خود تعادل تبدیل می شود ، این قسمت دوم از سوراخ است (شتاب سنج را بخوانید و یک موتور را برای تعادل خود کنترل کنید). قسمت اول فقط با ژیروسکوپ را می توانید در اینجا پیدا کنید. در این inst
