فهرست مطالب:
- مرحله 1: نصب کتابخانه
- مرحله 2: تبدیل فوریه و مفاهیم FFT
- مرحله 3: شبیه سازی یک سیگنال
- مرحله 4: تجزیه و تحلیل یک سیگنال شبیه سازی شده - کدگذاری
- مرحله 5: تجزیه و تحلیل یک سیگنال شبیه سازی شده - نتایج
- مرحله 6: تجزیه و تحلیل یک سیگنال واقعی - سیم کشی ADC
- مرحله 7: تجزیه و تحلیل یک سیگنال واقعی - کدگذاری
- مرحله 8: تجزیه و تحلیل یک سیگنال واقعی - نتایج
- مرحله 9: در مورد سیگنال سینوسی قطع شده چطور؟

تصویری: 1024 نمونه تجزیه و تحلیل طیف FFT با استفاده از مراحل Atmega1284: 9

2024 نویسنده: John Day | [email protected]. آخرین اصلاح شده: 2024-01-30 08:53


این آموزش نسبتاً آسان (با توجه به پیچیدگی این موضوع) به شما نشان می دهد که چگونه می توانید با استفاده از یک برد نوع آردوینو (1284 باریک) و پلاتر سریال ، یک تجزیه کننده طیف بسیار ساده 1024 نمونه بسازید. هر نوع برد سازگار با آردوینو انجام می دهد ، اما هرچه RAM بیشتری داشته باشد ، بهترین رزولوشن فرکانس را دریافت خواهید کرد. برای محاسبه FFT با 1024 نمونه به بیش از 8 کیلوبایت RAM نیاز دارد.
تجزیه و تحلیل طیف برای تعیین اجزای اصلی فرکانس یک سیگنال استفاده می شود. بسیاری از صداها (مانند صداهایی که توسط یک ساز موسیقی تولید می شوند) از یک فرکانس اساسی و برخی از هارمونیک ها تشکیل شده اند که دارای فرکانسی هستند که مضرب صحیح فرکانس اساسی است. تجزیه و تحلیل طیف همه این اجزای طیفی را به شما نشان می دهد.
ممکن است بخواهید از این تنظیمات به عنوان شمارنده فرکانس استفاده کنید یا هر نوع سیگنالی را که فکر می کنید نویز در مدار الکترونیکی شما وارد می کند ، بررسی کنید.
ما در اینجا روی بخش نرم افزار تمرکز می کنیم. اگر می خواهید یک مدار دائمی برای یک برنامه خاص ایجاد کنید ، باید سیگنال را تقویت و فیلتر کنید. این پیش شرط بندی کاملاً وابسته به سیگنالی است که می خواهید مطالعه کنید ، بسته به دامنه ، امپدانس ، حداکثر فرکانس و غیره … می توانید https://www.instructables.com/id/Analog-Sensor-Sig… را بررسی کنید.
مرحله 1: نصب کتابخانه
ما از کتابخانه ArduinoFFT نوشته شده توسط Enrique Condes استفاده خواهیم کرد. از آنجا که ما می خواهیم RAM را تا آنجا که ممکن است ذخیره کنیم ، از شاخه توسعه این مخزن استفاده می کنیم که اجازه می دهد از نوع داده شناور (به جای دو برابر) برای ذخیره داده های نمونه و محاسبه شده استفاده کند. بنابراین باید آن را به صورت دستی نصب کنیم. نگران نباشید ، فقط بایگانی را بارگیری کرده و آن را در پوشه کتابخانه Arduino خود فشرده نکنید (برای مثال در پیکربندی پیش فرض ویندوز 10: C: / Users / _your_user_name_ / Documents / Arduino / libraries)
با جمع آوری یکی از مثال های ارائه شده ، مانند "FFT_01.ino" ، می توانید بررسی کنید که کتابخانه به درستی نصب شده است.
مرحله 2: تبدیل فوریه و مفاهیم FFT
هشدار: اگر نمی توانید نماد ریاضی را مشاهده کنید ، ممکن است بخواهید به مرحله 3 بروید. در هر صورت ، اگر همه آن را دریافت نکرده اید ، فقط نتیجه گیری را در انتهای بخش در نظر بگیرید.
طیف فرکانس از طریق الگوریتم تبدیل سریع فوریه بدست می آید. FFT یک پیاده سازی دیجیتالی است که به مفهوم ریاضی تبدیل فوریه نزدیک می شود. بر اساس این مفهوم هنگامی که تکامل یک سیگنال را پس از یک محور زمانی دریافت می کنید ، می توانید نمایندگی آن را در یک حوزه فرکانسی ، متشکل از مقادیر پیچیده (واقعی + خیالی) ، بدانید. این مفهوم متقابل است ، بنابراین هنگامی که نمای حوزه دامنه فرکانس را می شناسید ، می توانید آن را به حوزه زمان برگردانید و سیگنال را دقیقاً مانند قبل از تبدیل دریافت کنید.
اما ما با این مجموعه از مقادیر پیچیده محاسبه شده در حوزه زمان چه می کنیم؟ خوب ، بیشتر آن به مهندسان واگذار می شود. برای ما یک الگوریتم دیگر می نامیم که این مقادیر پیچیده را به داده های چگالی طیفی تبدیل می کند: این مقدار (= شدت) مقدار مربوط به هر باند فرکانسی است. تعداد باند فرکانسی برابر با تعداد نمونه ها خواهد بود.
شما مطمئناً با مفهوم اکولایزر آشنا هستید ، مانند این ایده بازگشت به دهه 1980 با Graphic EQ. خوب ، ما نتایج مشابهی را به دست می آوریم اما با 1024 باند به جای 16 و وضوح بسیار بیشتر. هنگامی که اکولایزر نمای کلی موسیقی را ارائه می دهد ، تجزیه و تحلیل طیفی خوب به شما امکان می دهد شدت هر 1024 باند را دقیقاً محاسبه کنید.
یک مفهوم کامل ، اما:
- از آنجا که FFT یک نسخه دیجیتالی از تبدیل فوریه است ، سیگنال دیجیتال را تقریب زده و برخی اطلاعات را از دست می دهد. بنابراین ، به طور دقیق ، نتیجه FFT اگر با الگوریتم FFT معکوس به عقب تبدیل شود ، دقیقاً سیگنال اصلی را نمی دهد.
- همچنین این نظریه سیگنالی را در نظر می گیرد که محدود نیست ، اما یک سیگنال ثابت دائمی است. از آنجا که ما آن را فقط برای مدت زمان معینی (به عنوان مثال) دیجیتالی می کنیم ، خطاهای بیشتری معرفی می شود.
- در نهایت وضوح تبدیل آنالوگ به دیجیتال بر کیفیت مقادیر محاسبه شده تأثیر می گذارد.
در عمل
1) فرکانس نمونه برداری (ذکر شده fs)
ما یک سیگنال را نمونه گیری می کنیم ، یعنی دامنه آن را هر 1/fs ثانیه اندازه گیری می کنیم. fs فراوانی نمونه گیری است. به عنوان مثال اگر در 8 کیلوهرتز نمونه برداری کنیم ، ADC (مبدل آنالوگ به دیجیتال) که روی تراشه است هر 1/8000 ثانیه اندازه گیری می کند.
2) تعداد نمونه (N ذکر شده یا نمونه هایی در کد)
از آنجا که قبل از اجرای FFT باید همه مقادیر را بدست آوریم ، باید آنها را ذخیره کنیم و بنابراین تعداد نمونه ها را محدود می کنیم. الگوریتم FFT به تعدادی نمونه نیاز دارد که قدرت آنها 2 است. هرچه تعداد نمونه های بیشتر بهتر باشد اما حافظه زیادی را می طلبد ، بیشتر به ذخیره داده های تبدیل شده که مقادیر پیچیده ای هستند نیز نیاز داریم. کتابخانه Arduino FFT با استفاده از آن مقداری فضا را ذخیره می کند
- یک آرایه به نام "vReal" برای ذخیره داده های نمونه و سپس قسمت واقعی داده های تبدیل شده
- یک آرایه به نام "vImag" برای ذخیره قسمت فرضی داده های تبدیل شده
مقدار RAM مورد نیاز معادل 2 (آرایه) * 32 (بیت) * N (نمونه) است.
بنابراین در Atmega1284 ما که دارای 16 کیلوبایت رم خوب است حداکثر مقدار N = 16000*8 /64 = 2000 را ذخیره می کنیم. از آنجا که تعداد مقادیر باید توان 2 باشد ، حداکثر 1024 مقدار ذخیره می کنیم.
3) وضوح فرکانس
FFT برای تعداد باند فرکانس به عنوان تعداد نمونه مقادیر را محاسبه می کند. این نوارها از 0 HZ تا فرکانس نمونه برداری (fs) را شامل می شوند. بنابراین ، وضوح فرکانس به شرح زیر است:
رزولوشن = fs / N
وضوح تصویر وقتی کمتر است بهتر است. بنابراین برای وضوح بهتر (پایین) می خواهیم:
- نمونه های بیشتر و/یا
- a fs پایین تر
ولی…
4) حداقل fs
از آنجا که ما می خواهیم فرکانس های زیادی را ببینیم ، برخی از آنها بسیار بیشتر از "فرکانس اساسی" هستند ، نمی توانیم fs را خیلی پایین تنظیم کنیم. در واقع قضیه نمونه گیری Nyquist -Shannon وجود دارد که ما را مجبور می کند که فرکانس نمونه برداری بسیار بیشتر از دو برابر حداکثر فرکانسی که می خواهیم آزمایش کنیم داشته باشیم.
به عنوان مثال ، اگر بخواهیم تمام طیف از 0 هرتز تا 15 کیلوهرتز را تجزیه و تحلیل کنیم ، که تقریباً حداکثر فرکانسی است که اکثر مردم می توانند به طور واضح بشنوند ، باید فرکانس نمونه برداری را 30 کیلوهرتز تنظیم کنیم. در واقع متخصصان الکترونیک اغلب آن را در حداکثر 2.5 فرکانس (یا حتی 2.52) * قرار می دهند. در این مثال 2.5 * 15 KHz = 37.5 KHz خواهد بود. فرکانس نمونه برداری معمولی در صدای حرفه ای 44.1 کیلوهرتز (ضبط سی دی صوتی) ، 48 کیلوهرتز و بیشتر است.
نتیجه:
نکات 1 تا 4 منجر به: ما می خواهیم تا آنجا که ممکن است از نمونه ها استفاده کنیم. در مورد ما با یک دستگاه RAM 16 کیلوبایت ، ما 1024 نمونه را در نظر خواهیم گرفت. ما می خواهیم تا آنجا که ممکن است از کمترین فرکانس نمونه برداری استفاده کنیم ، تا زمانی که آنقدر بالا باشد که بتوانیم بالاترین فرکانس مورد انتظار در سیگنال خود را تجزیه و تحلیل کنیم (حداقل این فرکانس * 2.5 *).
مرحله 3: شبیه سازی یک سیگنال

در اولین تلاش خود ، ما نمونه TFT_01.ino که در کتابخانه آورده شده است را کمی تغییر می دهیم تا سیگنال متشکل از
- فرکانس اساسی ، 440 هرتز (موسیقی A)
- هارمونیک سوم با نصف قدرت اصلی ("-3 دسی بل")
- هارمونیک پنجم در 1/4 قدرت بنیادی ("-6 دسی بل)
در تصویر بالا سیگنال حاصله را مشاهده می کنید. در واقع بسیار شبیه یک سیگنال واقعی است که گاهی اوقات می توان در یک اسیلوسکوپ (که من آن را "بتمن" می نامم) در شرایطی که یک سیگنال سینوسی قطع می شود ، مشاهده کرد.
مرحله 4: تجزیه و تحلیل یک سیگنال شبیه سازی شده - کدگذاری
0) شامل کتابخانه
#شامل "arduinoFFT.h"
1) تعاریف
در بخش اعلانات ، ما داریم
const byte adcPin = 0؛ // A0
const uint16_t نمونه = 1024 ؛ // این مقدار باید همیشه توان 2 const uint16_t samplingFrequency = 8000 باشد؛ // بر حداکثر زمان سنج در timer_setup () SYSCLOCK/8/sampling تأثیر می گذارد فرکانس باید یک عدد صحیح باشد
از آنجا که سیگنال دارای 5 هارمونیک است (فرکانس این هارمونیک = 5 * 440 = 2200 هرتز) ما باید فرکانس نمونه برداری را بالاتر از 2.5 * 2200 = 5500 هرتز قرار دهیم. در اینجا من 8000 هرتز را انتخاب کردم.
ما همچنین آرایه هایی را که در آن داده های خام و محاسبه شده را ذخیره می کنیم ، اعلام می کنیم
float vReal [نمونه] ؛
float vImag [نمونه] ؛
2) تثبیت
ما یک شیء ArduinoFFT ایجاد می کنیم. نسخه توسعه دهنده ArduinoFFT از یک الگو استفاده می کند تا بتوانیم از نوع داده float یا double استفاده کنیم. Float (32 بیت) از نظر دقت کلی برنامه ما کافی است.
ArduinoFFT FFT = ArduinoFFT (vReal ، vImag ، نمونه ها ، نمونه گیری فرکانس) ؛
3) شبیه سازی سیگنال با پر کردن آرایه vReal ، به جای اینکه آن را با مقادیر ADC پر کنید.
در ابتدای حلقه ، آرایه vReal را با موارد زیر پر می کنیم:
چرخه های شناور = (((نمونه) * سیگنال فرکانس) / samplingFrequency) ؛ // تعداد چرخه های سیگنال که نمونه گیری می خواند
برای (uint16_t i = 0 ؛ i <نمونه ؛ i ++) {vReal = float ((دامنه * (sin ((i * (TWO_PI * چرخه)) / نمونه)))) ؛ / * ساخت داده با مثبت و ارزشهای منفی */ v += float ((دامنه * (sin ((5 * i * (TWO_PI * cycles))) / نمونه ها))) / 4.0) ؛ / * ساخت داده ها با مقادیر مثبت و منفی * / vImag = 0.0 ؛ // قسمت خیالی باید در صورت حلقه شدن صفر شود تا از محاسبات و سرریزهای اشتباه جلوگیری شود}
ما دیجیتالی شدن موج بنیادی و دو هارمونیک را با دامنه کمتر اضافه می کنیم. از آنجایی که آرایه خیالی را با صفر مقداردهی اولیه می کنیم. از آنجا که این آرایه توسط الگوریتم FFT پر شده است ، باید قبل از هر محاسبه جدید آن را دوباره پاک کنیم.
4) محاسبات FFT
سپس FFT و چگالی طیفی را محاسبه می کنیم
FFT.windowing (FFTWindow:: Hamming، FFTDirection:: Forward)؛
FFT.compute (FFTDirection:: Forward)؛ / * محاسبه FFT */ FFT.complexToMagnitude ()؛ / * محاسبه بزرگی */
عملیات FFT.windowing (…) داده های خام را تغییر می دهد زیرا FFT را روی تعداد محدودی از نمونه ها اجرا می کنیم. اولین و آخرین نمونه ها یک ناپیوستگی را نشان می دهند (در هیچ یک از آنها "هیچ چیز" وجود ندارد). این منبع خطا است. عملیات "پنجره سازی" تمایل دارد که این خطا را کاهش دهد.
FFT.compute (…) با جهت "Forward" تبدیل از دامنه زمان به حوزه فرکانس را محاسبه می کند.
سپس مقادیر قدر (یعنی شدت) را برای هر یک از باندهای فرکانس محاسبه می کنیم. آرایه vReal اکنون با مقادیر بزرگی پر شده است.
5) نقاشی پلاتر سریال
بیایید با فراخوانی تابع printVector مقادیر را در پلاتر سریال چاپ کنیم (…)
PrintVector (vReal ، (نمونه >> 1) ، SCL_FREQUENCY) ؛
این یک عملکرد عمومی است که به شما امکان می دهد داده ها را با محور زمان یا محور فرکانس چاپ کنید.
ما همچنین فرکانس باند را که بیشترین مقدار را دارد چاپ می کنیم
float x = FFT.majorPeak ()؛
Serial.print ("f0 =")؛ Serial.print (x، 6)؛ Serial.println ("هرتز") ؛
مرحله 5: تجزیه و تحلیل یک سیگنال شبیه سازی شده - نتایج

ما 3 سنبله مربوط به فرکانس اساسی (f0) ، هارمونیک 3 و 5 ، با نصف و 1/4 از قدر f0 ، همانطور که انتظار می رود را مشاهده می کنیم. ما می توانیم در بالای پنجره f0 = 440.430114 هرتز را بخوانیم. این مقدار دقیقاً 440 هرتز نیست ، به دلایلی که در بالا توضیح داده شد ، اما بسیار نزدیک به مقدار واقعی است. در واقع لازم نبود که این همه اعشار بی اهمیت را نشان دهد.
مرحله 6: تجزیه و تحلیل یک سیگنال واقعی - سیم کشی ADC

از آنجا که ما می دانیم چگونه از نظر تئوری باید پیش برویم ، ما می خواهیم یک سیگنال واقعی را تجزیه و تحلیل کنیم.
سیم کشی بسیار ساده است. خطوط را به یکدیگر و خط سیگنال را به پین A0 برد خود از طریق یک مقاومت سری با مقدار 1 کیلو اهم تا 10 کیلو اهم متصل کنید.
این مقاومت سری از ورودی آنالوگ محافظت می کند و از زنگ زدن جلوگیری می کند. باید تا آنجا که ممکن است برای جلوگیری از زنگ زدن ، و تا آنجا که ممکن است کم باشد تا جریان کافی برای شارژ سریع ADC فراهم شود. برای اطلاع از امپدانس مورد انتظار سیگنال متصل به ورودی ADC ، به برگه اطلاعات MCU مراجعه کنید.
برای این نسخه ی نمایشی ، من از یک ژنراتور عملکرد برای تغذیه یک سیگنال سینوسی با فرکانس 440 هرتز و دامنه حدود 5 ولت استفاده کردم (بهتر است دامنه بین 3 تا 5 ولت باشد بنابراین ADC در مقیاس کامل استفاده می شود) ، از طریق یک مقاومت 1.2 کیلو اهم. به
مرحله 7: تجزیه و تحلیل یک سیگنال واقعی - کدگذاری
0) شامل کتابخانه
#شامل "arduinoFFT.h"
1) اعلامیه ها و شروع
در بخش اعلامیه ، ورودی ADC (A0) ، تعداد نمونه ها و فرکانس نمونه برداری را مانند مثال قبلی تعریف می کنیم.
const byte adcPin = 0؛ // A0
const uint16_t نمونه = 1024 ؛ // این مقدار باید همیشه توان 2 const uint16_t samplingFrequency = 8000 باشد؛ // بر حداکثر زمان سنج در timer_setup () SYSCLOCK/8/sampling تأثیر می گذارد فرکانس باید یک عدد صحیح باشد
ما شیء ArduinoFFT را ایجاد می کنیم
ArduinoFFT FFT = ArduinoFFT (vReal ، vImag ، نمونه ها ، نمونه گیری فرکانس) ؛
2) تنظیم تایمر و ADC
ما تایمر 1 را طوری تنظیم می کنیم که در فرکانس نمونه برداری (8 کیلوهرتز) چرخه می زند و در مقایسه خروجی وقفه ایجاد می کند.
void timer_setup () {
// تنظیم مجدد تایمر 1 TCCR1A = 0؛ TCCR1B = 0 ؛ TCNT1 = 0 ؛ TCCR1B = بیت (CS11) | بیت (WGM12) ؛ // CTC ، پیش فروشنده 8 TIMSK1 = بیت (OCIE1B) ؛ OCR1A = ((16000000 /8) / samplingFrequency) -1 ؛ }
و ADC را طوری تنظیم کنید
- از A0 به عنوان ورودی استفاده می کند
- به طور خودکار در هر خروجی تایمر 1 خروجی B را مقایسه می کند
- با تبدیل کامل ، وقفه ایجاد می کند
کلاک ADC با تنظیم مجدد کلاک سیستم (16 مگاهرتز) با 16 در 1 مگاهرتز تنظیم شده است ، زیرا هر تبدیل تقریباً 13 ساعت در مقیاس کامل طول می کشد ، می توان تبدیل را با فرکانس 1/13 = 0.076 مگاهرتز = 76 کیلوهرتز 1/13 انجام داد. فرکانس نمونه برداری باید به طور قابل توجهی کمتر از 76 کیلوهرتز باشد تا ADC زمان نمونه برداری از داده ها را داشته باشد. (ما fs = 8 کیلوهرتز را انتخاب کردیم).
void adc_setup () {
ADCSRA = بیت (ADEN) | بیت (ADIE) | بیت (ADIF) ؛ // ADC را روشن کنید ، می خواهید در صورت اتمام وقفه ADCSRA | = بیت (ADPS2) ؛ // پیش فروشنده 16 ADMUX = بیت (REFS0) | (adcPin & 7) ؛ // تنظیم ورودی ADC ADCSRB = بیت (ADTS0) | بیت (ADTS2) ؛ // تایمر/شمارنده 1 مقایسه منبع ماشه Match ADCSRA | = bit (ADATE)؛ // روشن کردن راه اندازی خودکار}
ما کنترل کننده وقفه ای را که پس از هر تبدیل ADC برای ذخیره داده های تبدیل شده در آرایه vReal و پاکسازی وقفه فراخوانی می شود ، اعلام می کنیم.
// ADC ISR کامل
ISR (ADC_vect) {vReal [resultNumber ++] = ADC؛ if (resultNumber == نمونه) {ADCSRA = 0؛ // خاموش ADC}} EMPTY_INTERRUPT (TIMER1_COMPB_vect) ؛
می توانید توضیحی جامع در مورد تبدیل ADC در Arduino (analogRead) داشته باشید.
3) راه اندازی
در تابع راه اندازی ، جدول داده های تخیلی را پاک می کنیم و توابع زمان سنج و تنظیمات ADC را فرا می خوانیم
zeroI ()؛ // تابعی که همه داده های تخیلی را روی 0 تنظیم می کند - در قسمت قبل توضیح داده شد
timer_setup ()؛ adc_setup ()؛
3) حلقه
FFT.dcRemoval ()؛ // جزء DC این سیگنال را حذف کنید زیرا ADC به زمین اشاره شده است
FFT.windowing (FFTWindow:: Hamming، FFTDirection:: Forward)؛ // وزن داده ها FFT.compute (FFTDirection:: Forward)؛ // محاسبه FFT FFT.complexToMagnitude ()؛ // محاسبه مقادیر // چاپ طیف و فرکانس اساسی f0 PrintVector (vReal ، (نمونه >> 1) ، SCL_FREQUENCY) ؛ float x = FFT.majorPeak ()؛ Serial.print ("f0 =")؛ Serial.print (x، 6)؛ Serial.println ("هرتز") ؛
ما قطعه DC را حذف می کنیم زیرا ADC به زمین اشاره شده است و سیگنال تقریباً در حدود 2.5 ولت متمرکز شده است.
سپس داده ها را مطابق مثال قبلی محاسبه می کنیم.
مرحله 8: تجزیه و تحلیل یک سیگنال واقعی - نتایج

در واقع ما فقط یک فرکانس را در این سیگنال ساده می بینیم. فرکانس اساسی محاسبه شده 440.118194 هرتز است. در اینجا دوباره مقدار تقریبی بسیار نزدیک از فرکانس واقعی است.
مرحله 9: در مورد سیگنال سینوسی قطع شده چطور؟

حالا اجازه دهید کمی ADC را با افزایش دامنه سیگنال بالاتر از 5 ولت ، بیش از حد فعال کنیم ، بنابراین قطع می شود. بیش از حد فشار ندهید تا ورودی ADC از بین نرود!
ما می توانیم برخی از هارمونیک ها را نمایان کنیم. قطع سیگنال باعث ایجاد اجزای فرکانس بالا می شود.
شما اصول تجزیه و تحلیل FFT را در یک برد آردوینو مشاهده کرده اید. اکنون می توانید فرکانس نمونه برداری ، تعداد نمونه ها و پارامتر پنجره را تغییر دهید. کتابخانه همچنین برخی پارامترها را برای محاسبه سریعتر FFT با دقت کمتر اضافه می کند. متوجه خواهید شد که اگر فرکانس نمونه برداری را بسیار پایین تنظیم کنید ، بزرگی های محاسبه شده به دلیل تا شدن طیفی کاملاً اشتباه به نظر می رسند.
توصیه شده:
تجزیه و تحلیل داده های دما/رطوبت با استفاده از Ubidots و Google-Sheets: 6 مرحله

تجزیه و تحلیل داده های دما/رطوبت با استفاده از Ubidots و Google-Sheets: در این آموزش ، داده های مختلف دما و رطوبت را با استفاده از سنسور دما و رطوبت اندازه گیری می کنیم. همچنین نحوه ارسال این داده ها به Ubidots را خواهید آموخت. به طوری که می توانید آن را از هر کجا برای برنامه های مختلف تجزیه و تحلیل کنید. همچنین توسط sendin
چشمه رقص: آردوینو با تجزیه و تحلیل طیف MSGEQ7: 8 مرحله

Dancing Fountain: Arduino With MSGEQ7 Spectrum Analyzer: دریافت یک سیگنال صوتی و تبدیل آن به واکنش بصری یا مکانیکی بسیار جالب است. در این پروژه ما باید از Arduino Mega برای اتصال به تجزیه و تحلیل طیف MSGEQ7 استفاده کنیم که سیگنال صوتی ورودی را گرفته و باند را اجرا می کند
تجزیه و تحلیل امپدانس زیستی (BIA) با مراحل AD5933: 9
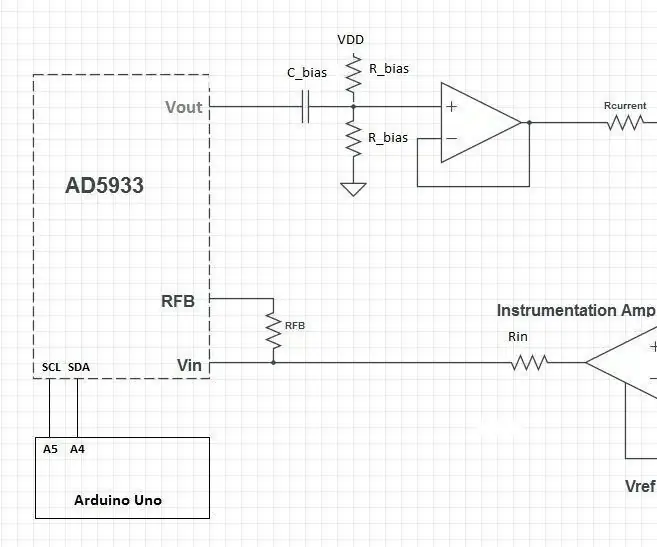
تجزیه و تحلیل امپدانس زیستی (BIA) با AD5933: من علاقه مند به ساختن یک تجزیه و تحلیل امپدانس زیستی برای اندازه گیری ترکیبات بدن بوده ام و جستجوهای تصادفی من همچنان یک طرح از کلاس ابزار دقیق پزشکی 2015 در دانشگاه واندربیلت پیدا کرده است. من روی طراحی کار کرده ام و
تجزیه و تحلیل نمونه سنگ: 4 مرحله

تجزیه و تحلیل نمونه سنگ: آنالیز نمونه سنگ برای شناسایی و تجزیه و تحلیل انواع نمونه سنگها با استفاده از تکنیک ارتعاش چکش نرم استفاده می شود. این یک روش جدید در شناسایی نمونه های سنگ است. اگر شهاب سنگ یا هر نمونه سنگ ناشناخته در آنجا باشد ، می توان تخمین زد
MCA تجزیه و تحلیل چند کاناله با آشکارساز طیف سنجی گاما NaI (Tl): 5 مرحله

MCA Multi Channel Analyzer with Gamma Spectroscopy NaI (Tl) Detector: سلام ، به همه کسانی که علاقه مند به سرگرمی طیف سنجی گاما هستند خوش آمدید. در این مقاله کوتاه ، من فقط می خواهم روند گزارش کار خود را برای ایجاد آشکارساز طیف سنجی گاما DIY خانگی با MCA به اشتراک بگذارم. این یک راهنما نیست ، من فقط عکسهای این روند را به اشتراک می گذارم. وقتی
